Lösung von Aufgabe 5.2 P (WS 13/14): Unterschied zwischen den Versionen
| Zeile 24: | Zeile 24: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | ich würde sagen, die Ungleichheitsrelation ist nicht transitiv, denn es gilt z.B. <math>1 \not= 2 </math> und <math> 2 \not= 1 </math> aber nicht <math> 1 \not= 1 </math> --[[Benutzer:Simon-2206|Mr.X]] ([[Benutzer Diskussion:Simon-2206|Diskussion]]) 13:08, 7. Feb. 2014 (CET) | + | *ich würde sagen, die Ungleichheitsrelation ist nicht transitiv, denn es gilt z.B. <math>1 \not= 2 </math> und <math> 2 \not= 1 </math> aber nicht <math> 1 \not= 1 </math> --[[Benutzer:Simon-2206|Mr.X]] ([[Benutzer Diskussion:Simon-2206|Diskussion]]) 13:08, 7. Feb. 2014 (CET) |
| − | + | **So ist es! --[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 18:35, 8. Feb. 2014 (CET) | |
<br /> | <br /> | ||
Aktuelle Version vom 8. Februar 2014, 18:35 Uhr
Entscheiden Sie für die folgenden Relationen, ob es sich um reflexive, symmetrische sowie transitive Relationen handelt?
- Parallelität von Geraden der Ebene
- Kongruenz geometrischer Figuren
- Teilbarkeit in
- Kleinerrelation in
- Größer-Gleich-Relation in
- Ungleichheit in
Lösungsvorschlag:
- r, s, t
- r, s, t
- r, t
- r, t
- r, (s), t
- r, s, t
r= reflexiv, s= Symmetrisch, t= transitiv
--Shaun das Schaf 12:03, 26. Nov. 2013 (CET)
- ich würde sagen, die Ungleichheitsrelation ist nicht transitiv, denn es gilt z.B.
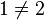und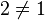 
aber nicht 
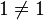--Mr.X (Diskussion) 13:08, 7. Feb. 2014 (CET)
- So ist es! --Tutorin Anne (Diskussion) 18:35, 8. Feb. 2014 (CET)
a) ist reflexiv, symmetrisch, transitiv
b) ist reflexiv, symmetrisch, transitiv
c) ist reflexiv und transitiv
d) ist transitiv
e) ist reflexiv und transitiv
f) ist symmetrisch und transitiv
--Smartie 15:44, 26. Nov. 2013 (CET)
Danke für eure Beiträge. Ich fasse zusammen:
a)-c) habt ihr identisch -die Antwort ist richtig.
d-e) seid ihr euch nicht einig. Hier bedarf es einer Begründung, weshalb ihr welche Eigenschaften gewählt habt. Ich mache ein Beispiel zu e):
Die Größer-Gleich-Relation in R ist nur reflexiv und transitiv, nicht aber symmetrisch. Symmetrisch wäre die Relation nur, wenn mit jedem Paar (a,b) auch das symmetrische Paar (b,a) enthalten wäre. Dies ist aber nicht der Fall. Z.B. 3 kleingleich 5--Tutorin Anne 11:06, 28. Nov. 2013 (CET)
