Benutzer:Matheschüler: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „(1) 250px (2) Datei:Geometrie …“)
 
Zeile 10: Zeile 10:
 
<br/>
 
<br/>
 
<br/>
 
<br/>
−
Die Berechnung des Volumens eines Kegelstumpfes beläuft sich auf die Subtraktiondes der Kegelspitze vom fiktiven Gesamtkegel.
+
Die Berechnung des Volumens eines Kegelstumpfes beläuft sich auf die Subtraktion der Kegelspitze vom fiktiven Gesamtkegel.
 
<br/>
 
<br/>
 
Hierbei gilt als Volumenformel für den Kegel: Grundfläche des Kegels multipliziert mit der Höhe des Kegels geteilt durch drei.
 
Hierbei gilt als Volumenformel für den Kegel: Grundfläche des Kegels multipliziert mit der Höhe des Kegels geteilt durch drei.
Zeile 43: Zeile 43:
 
<br />
 
<br />
 
<math> V = \frac{\sin(\alpha) \cdot \pi}{3} \cdot (r_{G_{K}}^2 \cdot r_{M_{0}} - r_{G_{S}}^2 \cdot r_{M_{1}}) </math>
 
<math> V = \frac{\sin(\alpha) \cdot \pi}{3} \cdot (r_{G_{K}}^2 \cdot r_{M_{0}} - r_{G_{S}}^2 \cdot r_{M_{1}}) </math>
 +
<br />
 +
<br />
 +
Bild (2) zeigt übrigens auch noch Quader und einen Zylinder.

Version vom 2. Mai 2014, 20:30 Uhr

(1) Das Bild zeigt eine Deckenlampe, die an meiner Decke hängt. Aufnahme von schräg unten. (2) Das Bild zeigt einen Plattenspieler. Es soll Startknopf, Powerschalter und Drehteller als geometrische Gebilde hervorheben.

Bild (1) und Bild (2) haben die Gemeinsamkeit, dass sie beide einen Kegelstumpf zeigen.
(1) von schräg unten
(2) von schräg oben

Die Berechnung des Volumens eines Kegelstumpfes beläuft sich auf die Subtraktion der Kegelspitze vom fiktiven Gesamtkegel.
Hierbei gilt als Volumenformel für den Kegel: Grundfläche des Kegels multipliziert mit der Höhe des Kegels geteilt durch drei.
Kegel: 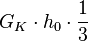G_{K} \cdot h_{0} \cdot \frac{1}{3}
analog gilt für die Spitze: 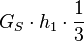G_{S} \cdot h_{1} \cdot \frac{1}{3}
Die Höhe wiederum lässt sich mithilfe der Winkelfunktionen berechnen. Es gilt hier
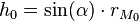
h_{0} = \sin(\alpha) \cdot r_{M_{0}}
Der Winkel \alpha ist der Neigungswinkel zwischen dem Mantel des Kegels und der Grundfläche.
Den Radius des ausgebreiteten Mantels (also die Hypothenuse des zur Hilfe gezogenen rechtwinkligen Dreiecks) habe ich mit 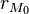r_{M_{0}} bezeichnet.

Am Ende erhalten wir also eine allgemeine Formel

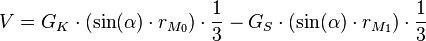
V = G_{K} \cdot (\sin(\alpha) \cdot r_{M_{0}}) \cdot \frac{1}{3} - G_{S} \cdot (\sin(\alpha) \cdot r_{M_{1}}) \cdot \frac{1}{3}

oder besser:

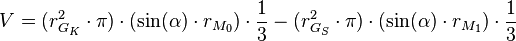
V = (r_{G_{K}}^2 \cdot \pi) \cdot (\sin(\alpha) \cdot r_{M_{0}}) \cdot \frac{1}{3} - (r_{G_{S}}^2 \cdot \pi) \cdot (\sin(\alpha) \cdot r_{M_{1}}) \cdot \frac{1}{3}

und in kurz:

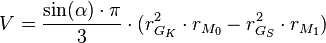
V = \frac{\sin(\alpha) \cdot \pi}{3} \cdot (r_{G_{K}}^2 \cdot r_{M_{0}} - r_{G_{S}}^2 \cdot r_{M_{1}})

Bild (2) zeigt übrigens auch noch Quader und einen Zylinder.

Von „http://geometrie.zum.de/index.php?title=Benutzer:Matheschüler&oldid=26290“