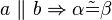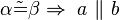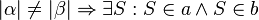Lösung von Aufgabe 3.3 (SoSe 14): Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 18: | Zeile 18: | ||
Deine Antwort ist schon ganz gut. 3. hat einen Zusammenhang zum Stufenwinkelsatz. Welche der 4 Aussagen sind nun aequivalent zum Stufenwinkelsatz?--[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 16:42, 14. Mai 2014 (CEST) | Deine Antwort ist schon ganz gut. 3. hat einen Zusammenhang zum Stufenwinkelsatz. Welche der 4 Aussagen sind nun aequivalent zum Stufenwinkelsatz?--[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 16:42, 14. Mai 2014 (CEST) | ||
[[Category:Einführung_P]] | [[Category:Einführung_P]] | ||
| + | Ich würde sagen das Aussage Nr.3 auch äquivalent zum Stufenwinkelsatz ist. Sie repräsentiert einen indirekten Beweis durch Kontraposition, | ||
| + | nähmlich dass die Winkel |α| und |β| nicht gleich groß sind wenn die Geraden a und b nicht parallel zueinander sind.--[[Benutzer:Shaman|Shaman]] ([[Benutzer Diskussion:Shaman|Diskussion]]) 16:44, 18. Mai 2014 (CEST)<br /> | ||
| + | Shaman, das ist richtig! Sehr gut.--[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 16:38, 20. Mai 2014 (CEST) | ||
| + | <br /> | ||
| + | Entschuldigt, eine "unerfahrene" Frage: Was bedeutet das ist-gleich Zeichen mit Schlangelinie darüber? Kann ja nicht "ungefähr-ist-gleich" heißen. DANKE!! (Pippilotta)<br /> | ||
| + | Das Zeichen bedeutet kongruent zu. Zwei Winkel sind kongruent, wenn sie gleich groß sind. Zwei Seiten sind kongruent, wenn sie gleich lang sind. --[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 19:17, 16. Mai 2014 (CEST)<br /> | ||
| − | + | Meiner Meinung nach die Aussage Nr. 4 ist die Äquivalenzaussagen zum Stufenwinkelsatz, damit auch ein Kriterium für eine hinreichende und notwendige Bedingung. | |
| − | + | Werde versuchen die Nr. 3 zu übersetzen. Die Winkel |α| und |β| sind nicht gleich, daraus folgt, dass ein Punkt S existiert, der Element von der Gerade a und Gerade b ist. Bin mir nicht sicher aber kann sein, dass es damit gemeint ist, dass die eine Gerade die andere im Punkt S schneidet?--[[Benutzer:Picksel|Picksel]] ([[Benutzer Diskussion:Picksel|Diskussion]]) 18:20, 18. Mai 2014 (CEST)<br /> | |
| − | + | Picksel, 4. ist eine Äquivalenzaussage. Richtig. Nicht aber eine äquivalente Aussage zum Stufenwinkelsatz. 3. hast du richtig übersetzt. Es heißt einfach, dass sich die Geraden schneiden. --[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 16:38, 20. Mai 2014 (CEST) | |
Aktuelle Version vom 20. Mai 2014, 15:38 Uhr
a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
Stufenwinkelsatz: Wenn zwei parallele Geraden a und b von einer dritten Gerade c geschnitten werden, so sind die auftretenden Stufenwinkel gleich groß. --MarieSo (Diskussion) 18:15, 12. Mai 2014 (CEST)
Stufenwinkelsatz: Stufenwinkel sind gleich groß genau dann, wenn sie an parallelen Geraden liegen.--Früchtchen:) (Diskussion) 09:19, 15. Mai 2014 (CEST)
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel  und
und  . Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äquivalente Aussage (Begründen Sie jeweils)?
. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äquivalente Aussage (Begründen Sie jeweils)?
1. repräsentiert den Stufenwinkelsatz 2. ist eine Umkehrung des Stufenwinkelsatz 3. kein Zusammenhang zum Stufenwinkelsatz? 4. ist eine Äquivalenzaussage zum Stufenwinkelsatz --MarieSo (Diskussion) 18:15, 12. Mai 2014 (CEST)
Deine Antwort ist schon ganz gut. 3. hat einen Zusammenhang zum Stufenwinkelsatz. Welche der 4 Aussagen sind nun aequivalent zum Stufenwinkelsatz?--Tutorin Anne (Diskussion) 16:42, 14. Mai 2014 (CEST)
Ich würde sagen das Aussage Nr.3 auch äquivalent zum Stufenwinkelsatz ist. Sie repräsentiert einen indirekten Beweis durch Kontraposition, nähmlich dass die Winkel |α| und |β| nicht gleich groß sind wenn die Geraden a und b nicht parallel zueinander sind.--Shaman (Diskussion) 16:44, 18. Mai 2014 (CEST)
Shaman, das ist richtig! Sehr gut.--Tutorin Anne (Diskussion) 16:38, 20. Mai 2014 (CEST)
Entschuldigt, eine "unerfahrene" Frage: Was bedeutet das ist-gleich Zeichen mit Schlangelinie darüber? Kann ja nicht "ungefähr-ist-gleich" heißen. DANKE!! (Pippilotta)
Das Zeichen bedeutet kongruent zu. Zwei Winkel sind kongruent, wenn sie gleich groß sind. Zwei Seiten sind kongruent, wenn sie gleich lang sind. --Tutorin Anne (Diskussion) 19:17, 16. Mai 2014 (CEST)
Meiner Meinung nach die Aussage Nr. 4 ist die Äquivalenzaussagen zum Stufenwinkelsatz, damit auch ein Kriterium für eine hinreichende und notwendige Bedingung.
Werde versuchen die Nr. 3 zu übersetzen. Die Winkel |α| und |β| sind nicht gleich, daraus folgt, dass ein Punkt S existiert, der Element von der Gerade a und Gerade b ist. Bin mir nicht sicher aber kann sein, dass es damit gemeint ist, dass die eine Gerade die andere im Punkt S schneidet?--Picksel (Diskussion) 18:20, 18. Mai 2014 (CEST)
Picksel, 4. ist eine Äquivalenzaussage. Richtig. Nicht aber eine äquivalente Aussage zum Stufenwinkelsatz. 3. hast du richtig übersetzt. Es heißt einfach, dass sich die Geraden schneiden. --Tutorin Anne (Diskussion) 16:38, 20. Mai 2014 (CEST)