Übung 24.11.14: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe II.04) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe II.05) |
||
| Zeile 28: | Zeile 28: | ||
Entwickeln Sie eine Parameterdarstellung von <math>e</math>. | Entwickeln Sie eine Parameterdarstellung von <math>e</math>. | ||
= Aufgabe II.05 = | = Aufgabe II.05 = | ||
| − | Gegeben seien die Gerade <math>l</math> durch die Geradengleichung <math>y(x)=-\frac{1}{4}</math> und der Punkt <math>F(0,\frac{1}{4}</math>. Es sei | + | Gegeben seien die Gerade <math>l</math> durch die Geradengleichung <math>y(x)=-\frac{1}{4}</math> und der Punkt <math>F \left(0,\frac{1}{4} \right)</math>. Es sei <math>L_i</math> eine Folge von Punkten auf <math>l</math>. |
<!--- hier drunter nichts eintragen ---> | <!--- hier drunter nichts eintragen ---> | ||
[[Kategorie:Linalg]] | [[Kategorie:Linalg]] | ||
Version vom 13. November 2014, 13:57 Uhr
Aufgabe II.01Stellen Sie eine Parameterdarstellung für Archimedische Spirale aus Abbildung II.01 auf. Abb. II.01 Aufgabe II.02Wir beziehen uns wieder auf Abb. II.01. Es sei Aufgabe II.03Als Parameter für die Darstellung logarithmischer Spiralen sei die Zeit Aufgabe II.04Bei der Evolventenverzahnung von Zahnrädern sind die Zahnflanken der Zahnräder Teile von sogenannten Kreisevolventen. Es sei Entwickeln Sie eine Parameterdarstellung von Aufgabe II.05Gegeben seien die Gerade |
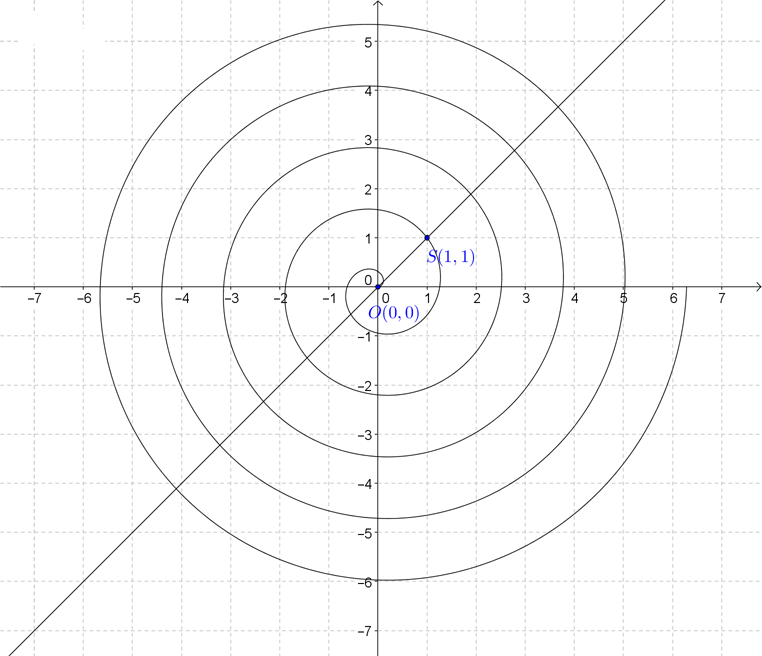
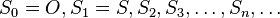 die Folge der Schnittpunkte von
die Folge der Schnittpunkte von 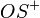 mit der archimedischen Spirale.
mit der archimedischen Spirale. 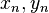 dieser Schnittpunktfolge an.
dieser Schnittpunktfolge an.
 gewählt. Negative Zeiten seien nicht zugelassen. Begründen Sie: Alle logarithmischen Spiralen starten in dem Punkt
gewählt. Negative Zeiten seien nicht zugelassen. Begründen Sie: Alle logarithmischen Spiralen starten in dem Punkt 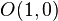 .
.
 eine Garnrolle, die wir als Kreis modellieren. Auf
eine Garnrolle, die wir als Kreis modellieren. Auf  aufgewickelt, der den Anfangspunkt
aufgewickelt, der den Anfangspunkt  haben möge. Wir nehmen
haben möge. Wir nehmen  bezüglich
bezüglich  durch die Geradengleichung
durch die Geradengleichung 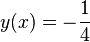 und der Punkt
und der Punkt 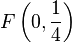 . Es sei
. Es sei 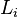 eine Folge von Punkten auf
eine Folge von Punkten auf 
