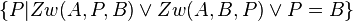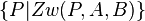Strahlen bzw. Halbgeraden SoSe 13: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Definition II.5: (Halbgerade, bzw. Strahl))
 
(Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt)
Zeile 15: Zeile 15:
 
===== Definition II.5: (Halbgerade, bzw. Strahl) =====
 
===== Definition II.5: (Halbgerade, bzw. Strahl) =====
 
(Ergänzen Sie die fehlenden Teile selbst.)<br />
 
(Ergänzen Sie die fehlenden Teile selbst.)<br />
−
{{Definition|'''offene Halbgerade <math>AB^+</math>'''<br />Es sei <math>AB</math> eine Gerade. Unter der offenen Halbgeraden <math>AB^+</math> versteht man  die Menge aller Punkte <math>P</math> für die gilt: <br />(a) Zw(A,P,B) <br /> oder <br />(b) Zw(A,B,P)<br />Der Punkt <math>A</math> heißt Anfangspunkt von <math>AB^+</math>.}}
+
{{Definition|'''offene Halbgerade <math>AB^+</math>'''<br />Es sei <math>AB</math> eine Gerade. Unter der offenen Halbgeraden <math>AB^+</math> versteht man  die Menge aller Punkte <math>P</math> für die gilt: <math>\{P|Zw(A,P,B) \lor Zw(A,B,P) \lor P=B \}</math>}}
−
{{Definition|'''offene Halbgerade <math>AB^-</math>'''<br />Es sei <math>AB</math> eine Gerade. Unter der offenen Halbgeraden <math>AB^-</math> versteht man  die Menge aller Punkte <math>P</math> für die gilt: Zw (P,A,B) <br />Der Punkt <math>A</math> heißt Anfangspunkt von <math>AB^-</math>.}}
+
{{Definition|'''offene Halbgerade <math>AB^-</math>'''<br />Es sei <math>AB</math> eine Gerade. Unter der offenen Halbgeraden <math>AB^-</math> versteht man  die Menge aller Punkte <math>P</math> für die gilt: <math>\{P|Zw(P,A,B)\}</math>}}
−
{{Definition|'''Halbgeraden <math>AB^+</math> bzw. <math>AB^-</math>'''<br /> Es sei <math>AB</math> eine Gerade. Unter den Halbgeraden <math>AB^+</math> bzw. <math>AB^-</math> versteht man die offenen Halbgeraden <math>AB+</math> bzw. <math>AB^-</math> jeweils vereinigt mit den Punkten A und B. }}<br/>
+
{{Definition|'''Halbgeraden <math>AB^+</math> bzw. <math>AB^-</math>'''<br /> Es sei <math>AB</math> eine Gerade. Unter den Halbgeraden <math>AB^+</math> bzw. <math>AB^-</math> versteht man die offenen Halberaden vereinigt mit dem Punkt A. }}<br/>
  
  

Aktuelle Version vom 21. November 2014, 15:08 Uhr

Halbgeraden bzw. Strahlen

Geogebra-App
  • Verschieben Sie P auf AB
  • Manipulieren Sie A und B für eine andere Lage der Geraden AB


Definition II.5: (Halbgerade, bzw. Strahl)

(Ergänzen Sie die fehlenden Teile selbst.)

Definition

offene Halbgerade AB^+
Es sei AB eine Gerade. Unter der offenen Halbgeraden AB^+ versteht man die Menge aller Punkte P für die gilt: \{P|Zw(A,P,B) \lor Zw(A,B,P) \lor P=B \}

Definition

offene Halbgerade AB^-
Es sei AB eine Gerade. Unter der offenen Halbgeraden AB^- versteht man die Menge aller Punkte P für die gilt: \{P|Zw(P,A,B)\}

Definition

Halbgeraden AB^+ bzw. AB^-
Es sei AB eine Gerade. Unter den Halbgeraden AB^+ bzw. AB^- versteht man die offenen Halberaden vereinigt mit dem Punkt A.



Von „http://geometrie.zum.de/index.php?title=Strahlen_bzw._Halbgeraden_SoSe_13&oldid=27105“