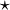|
|
| (12 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| − | == Formatierungshilfen und -erinnerungen ==
| + | :::::<math>\star</math><br /> |
| − | [http://wiki.zum.de/Hilfe:TeX Hilfe zu LaTeX]<br />
| + | [[Datei:Sternchen blau.png]] |
| | | | |
| | | | |
| − | {| class="wikitable"
| + | == Formatierungshilfen == |
| − | |-
| + | [http://wiki.zum.de/Hilfe:TeX Hilfe zu LaTeX]<br /> |
| − | | '''Schritt''' || '''Begründung'''
| + | <math>\varphi</math> (dieses kleine phi heißt \varphi) |
| − | |-
| + | |
| − | |1)
| + | |
| − | ||Voraussetzung
| + | |
| − | |-
| + | |
| − | |2)
| + | |
| − | ||(1)
| + | |
| − | |-
| + | |
| − | |3)
| + | |
| − | ||
| + | |
| − | |-
| + | |
| − | |4)
| + | |
| − | ||
| + | |
| − | |-
| + | |
| − | |5)
| + | |
| − | ||
| + | |
| − | |-
| + | |
| − | |6)
| + | |
| − | ||
| + | |
| − | |}
| + | |
| | | | |
| | {| class="wikitable " | | {| class="wikitable " |
| Zeile 52: |
Zeile 33: |
| | | Element | | | Element |
| | |} | | |} |
| − |
| |
| − | <br />
| |
| − | == Kleine Zusammenfassungen ==
| |
| − | === Klasseneinteilung ===
| |
| − | :Es sei <math>M</math> eine Menge und <math>K=\{ T_1, T_2, T_3, ..., T_n, ...\} </math> eine Menge von Teilmengen von <math>M</math>.
| |
| − | :<math>K</math> ist eine Klasseneinteilung von <math>M</math>, wenn gilt:
| |
| − | :# notwendige Bedingung 1: Keine der Teilmengen ist die leere Menge.
| |
| − | :# notwendige Bedingung 2: Je zwei Teilmengen sind disjunkt.
| |
| − | :# notwendige Bedingung 3: Die Vereinigung aller Teilmengen ergibt wieder die Menge <math>M</math>.
| |
| − | ::Mengen sind disjunkt, wenn die Schnittmenge dieser Mengen die leere Menge ist, bzw. die Mengen keine gemeinsamen Objekte besitzen.<br />
| |
| − | === Relationen ===
| |
| − | <u>Definition: (n-stellige Relation)</u>
| |
| − | :Es seien <math> M_1,\ M_2,\ M_3,\ ...,\ M_n\ n</math> Mengen, wobei keine dieser Mengen die leere Menge ist. Jede Teilmenge aus <math> M_1 \times M_2 \times M_3 ...\times M_n </math> ist eine <math>\ n-</math>stellige Relation.<br />
| |
| − | <u>Definition: (Äquivalenzrelation)</u>
| |
| − | :Eine Relation <math>\ R</math> in einer Menge <math>\ M</math> heißt ''Äquivalenzrelation'', wenn sie reflexiv, symmetrisch und transitiv ist.<br />
| |
| − |
| |
| − | == Versuch einer Auflistung ==
| |
| − |
| |
| − | ==== Axiome ====
| |
| − | =====AXIOM I/0=====
| |
| − | :Geraden und Ebenen sind Punktmengen.
| |
| − | =====AXIOM I/1(Axiom von der Geraden)=====
| |
| − | :Zu zwei beliebigen verschiedenen Punkten gibt es genau eine Gerade, die die beiden Punkte enthält.
| |
| − | =====AXIOM I/2=====
| |
| − | :Zu jeder Geraden gibt es wenigstens zwei Punkte, die dieser Geraden angehören.
| |
| − | =====AXIOM I/3=====
| |
| − | :Es gibt wenigstens 3 Punkte, die nicht kollinear sind.
| |
| − | =====Axiom I/4=====
| |
| − | :Zu je drei nichtkollinearen Punkten gibt es genau eine Ebene, die diese drei Punkte enthält. Jede Ebene enthält (wenigstens) einen Punkt.
| |
| − | =====Axiom I/5=====
| |
| − | :Wenn zwei Punkte einer Geraden ''g'' in einer Ebene ''E ''liegen, so gehört g zu ''E''.
| |
| − | =====Axiom I/6=====
| |
| − | :Wenn zwei Ebenen einen Punkt gemeinsam haben, so haben sie noch mindestens einen weiteren Punkt gemeinsam.
| |
| − | =====Axiom I/7=====
| |
| − | :Es gibt vier Punkte, die nicht komplanar sind.
| |
| − | ===== Axiom II.1: (Abstandsaxiom) =====
| |
| − | :Zu je zwei Punkten <math>\ A</math> und <math>\ B</math> gibt es eine eindeutig bestimmte nicht negative reelle Zahl <math>\ d</math> mit <math>d=0:\Longleftrightarrow A=B</math>.
| |
| − | ===== Axiom II.2: =====
| |
| − | :Für zwei beliebige Punkte <math>\ A</math> und <math>\ B</math> gilt <math>\left| AB \right| = \left| BA \right|</math>.
| |
| − | ===== Axiom II/3: (Dreiecksungleichung) =====
| |
| − | :Für drei beliebige Punkte <math>\ A, B</math> und <math>\ C</math> gilt: <math>\left|AB \right|+ \left| BC \right| \geq \left| AC \right|.</math>
| |
| − | ===== Axiom III.1: (Axiom vom Lineal) =====
| |
| − | :Zu jeder nicht negativen reelen Zahl <math>\ d</math> gibt es auf jedem Strahl <math>\ p</math> genau einen Punkt, der zum Anfangspunkt von <math>\ p</math> den Abstand <math>\ d</math> hat.
| |
| − |
| |
| − | ==== Definitionen ====
| |
| − | =====Definition I/2: (kollinear)=====
| |
| − | :Eine Menge von Punkten heißt kollinear, wenn es eine Gerade gibt, die alle Punkte der Menge enthält.
| |
| − | :Schreibweise: koll(''A, B, C,'' ...) Sollten die Punkte ''A, B, C'' einer Menge nicht kollinear sein, so schreibt man:nkoll(''A, B, C)''
| |
| − | =====Definition I/3: (Inzidenz Punkt Ebene)=====
| |
| − | :Ein Punkt ''P'' inzidiert mit einer Ebene ''E'', wenn ''P'' ein Element der Ebene ''E'' ist.
| |
| − | =====Definition I/4: (Inzidenz Gerade Ebene)=====
| |
| − | :Eine Gerade ''g'' gehört zu einer Ebene ''E'', wenn jeder Punkt von ''g'' zu ''E'' gehört.
| |
| − | =====Definition I/5: (Raum)=====
| |
| − | :Die Menge aller Punkte P wird Raum genannt.
| |
| − | =====Definition I/6: (komplanar)=====
| |
| − | :Eine Menge von Punkten heißt komplanar, wenn es eine Ebene gibt, die alle Punkte der Menge enthält. Schreibweise: komp(''A'', ''B'', ''C, D, ...'') (analog nkomp(..) für nicht komplanar)
| |
| − | =====Definition I/7: (komplanar für Geraden)=====
| |
| − | :Zwei Geraden'' g ''und ''h'' sind komplanar, wenn es eine Ebene gibt, in der beide Geraden vollständig liegen.
| |
| − | :Schreibweise: komp(g, h)
| |
| − | =====Definition I/8: (Geradenparallelität)=====
| |
| − | :Zwei Geraden ''g'' und ''h'' sind parallel, wenn sie identisch oder komplanar und schnittpunktfrei sind.
| |
| − | :In Zeichen: ''g''||''h''.
| |
| − | =====Definition I/9: (windschief )=====
| |
| − | :Zwei Geraden ''g'' und ''h'' sind windschief, wenn sie schnittpunktfrei und nicht parallel sind.
| |
| − | =====Definition I/10: (parallel für Ebenen)=====
| |
| − | :Zwei Ebene ''E''<sub>1</sub> und ''E''<sub>2</sub> sind parallel, wenn sie keinen Punkt gemeinsam haben.
| |
| − | ===== Definition II.1: (Abstand) =====
| |
| − | :Der Abstand zweier Punkte <math>\ A</math> und <math>\ B</math> ist die Zahl, die nach dem Abstandsaxiom den Punkten <math>\ A</math> und <math>\ B</math> zugeordnet werden kann. <br />Schreibweise: <math>d = \left| AB \right|</math>.
| |
| − | ===== Definition II.1: (Zwischenrelation) =====
| |
| − | :Ein Punkt <math>\ B</math> liegt zwischen zwei Punkten <math>\ A</math> und <math>\ C</math>, wenn <math> \left| AB \right| + \left| BC \right| = \left| AC \right| </math> gilt und der Punkt <math>\ B</math> sowohl von <math>\ A</math> als auch von <math>\ C</math> verschieden ist.
| |
| − | :Schreibweise: <math> \operatorname{Zw} \left( A, B, C \right) </math>
| |
| − | ===== Definition II.2: (Strecke, Endpunkte einer Strecke) =====
| |
| − | :
| |
| − | ===== Definition II.3: (Länge einer Strecke) =====
| |
| − | :
| |
| − | ===== Definition II.3: (Halbgerade, bzw. Strahl) =====
| |
| − | ::[[Lösung_von_Aufgabe_6.5]]
| |
| − | ::[[Lösung_von_Aufgabe_6.6]]
| |
| − | ===== Definition III.1: (Mittelpunkt einer Strecke) =====
| |
| − | :Wenn ein Punkt <math>\ M</math> der Strecke <math>\overline{AB}</math> zu den Endpunkten <math>\ A</math> und <math>\ B</math> jeweils den selben Abstand hat, dann ist er der Mittelpunkt der Strecke <math>\overline{AB}</math>.
| |
| − |
| |
| − | ==== Sätze ====
| |
| − | =====Satz I.1=====
| |
| − | :Es seien ''g'' und ''h'' zwei Geraden. Wenn ''g'' und ''h'' nicht identisch sind, haben sie höchstens einen Punkt gemeinsam.
| |
| − | =====Satz I.2: (Kontraposition von Satz I.1)=====
| |
| − | :Es seien ''g'' und ''h'' zwei Geraden.
| |
| − | :Wenn ''g'' und ''h'' mehr als einen Punkt gemeinsam haben, so sind ''g'' und ''h'' identisch.
| |
| − | ===== Satz I.3: (Existenz von drei Geraden)=====
| |
| − | :Es existieren mindestens drei paarweise verschiedene Geraden.
| |
| − | =====Satz I.5:=====
| |
| − | :Zwei voneinander verschiedene Ebenen haben entweder keinen Punkt oder eine Gerade gemeinsam, auf der alle gemeinsamen Punkte beider Ebenen liegen.
| |
| − | =====Satz I.6:=====
| |
| − | :Eine Ebene und eine nicht in ihr liegende Gerade haben höchstens einen Punkt gemeinsam.
| |
| − | =====Satz I.7:=====
| |
| − | :Jede Ebene enthält (wenigstens) drei Punkte.
| |
| − | ===== Satz II.1 =====
| |
| − | :Aus <math> \operatorname{Zw} \left( A, B, C \right) </math> folgt <math> \operatorname{Zw} \left( C, B, A \right) </math>.
| |
| − | ===== Satz II.2: =====
| |
| − | :Aus <math> \operatorname{Zw} \left( A, B, C \right) </math> folgt <math> \operatorname{koll} \left( A, B, C \right) </math>.
| |
| − | ===== Satz II.3 =====
| |
| − | :Es sei <math> \operatorname{koll} \left( A, B, C \right) </math> mit <math>\ A, B, C</math> sind paarweise verschieden.<br /> Dann gilt <math> \operatorname{Zw} \left( A, B, C \right) </math> oder <math> \operatorname{Zw} \left( A, C, B \right) </math> oder <math> \operatorname{Zw} \left( B, A, C \right) </math>.
| |
| − | ===== Satz II.4 =====
| |
| − | :Es sei <math>\ O</math> ein Punkt einer Geraden <math>\ g</math>. <br />Die Teilmengen <math> \ OA^+ \setminus \left\{ O \right\}</math>, <math> \left\{ O \right\}</math> und <math> \ OA^- \setminus \left\{ O \right\}</math> bilden eine Klasseneinteilung der Geraden <math>\ g</math>.
| |
| − | ===== Satz III.1: (Existenz und Eindeutigkeit des Mittelpunkte einer Strecke) =====
| |
| − | :Jede Strecke hat genau einen Mittelpunkt.
| |
 (dieses kleine phi heißt \varphi)
(dieses kleine phi heißt \varphi)