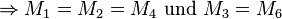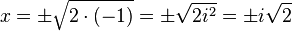Lösung von Aufgabe 1.2 (WS 16 17): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 101: | Zeile 101: | ||
Gruß Alex | Gruß Alex | ||
| − | + | Ja, im Prinzip hab ich das genauso wie [[Benutzer:AndyWeber|AJWeber]] gemacht. Nur eben nicht meine Zwischenschritte aufgeschrieben, | |
weil die Aufgaben (noch) so einfach sind, dass es gar nicht so viele Zwischenschritte gibt. In einer Klausur würde ich das etwas ausführlicher aufschreiben und bei den anderen Aufgaben | weil die Aufgaben (noch) so einfach sind, dass es gar nicht so viele Zwischenschritte gibt. In einer Klausur würde ich das etwas ausführlicher aufschreiben und bei den anderen Aufgaben | ||
der ersten Woche habe ich mich auch etwas ausführlicher über die Begründung ausgelassen <span style="font-size:150%">😉</span>, | der ersten Woche habe ich mich auch etwas ausführlicher über die Begründung ausgelassen <span style="font-size:150%">😉</span>, | ||
Aktuelle Version vom 27. Oktober 2016, 18:41 Uhr
Geben Sie eine andere Schreibweise der folgenden Mengen an und prüfen Sie, welche Mengen identisch sind.
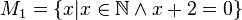
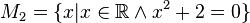
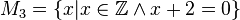
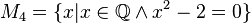
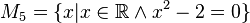
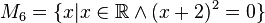
sehr schöne Lösungen, prima!--Schnirch (Diskussion) 13:27, 25. Okt. 2016 (CEST)
Hallo ;)
AlanTu deine Lösugnen sind richtig nur wie kommst du darauf? In den ersten Übungen sieht das auch noch recht einfach aus und man kann vieles im Kopf berechnen, jedoch musst du alles auch immer belegen und beweisen. Schau mal bei AJWeber, da passt alles ;)
Gruß Alex
Ja, im Prinzip hab ich das genauso wie AJWeber gemacht. Nur eben nicht meine Zwischenschritte aufgeschrieben, weil die Aufgaben (noch) so einfach sind, dass es gar nicht so viele Zwischenschritte gibt. In einer Klausur würde ich das etwas ausführlicher aufschreiben und bei den anderen Aufgaben der ersten Woche habe ich mich auch etwas ausführlicher über die Begründung ausgelassen 😉, bei der Aufgabe wollte ich mich dann halt etwas kürzer fassen. --AlanTu (Diskussion) 20:01, 24. Okt. 2016 (CEST)
Eine sehr schöne Lösung, nur eine kleine Anmerkung wenn wir schon bei den komplexen Zahlen sind:
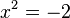
mit
folgt:
P.S. Sei froh, dass wir hier nicht zuvor in die Polarform umwandeln müssen um die Wurzel aus komplexen Zahlen ziehen zu können.
Glaub mir, das macht keinen Spaß ;P Gruß Alex --Tutor: Alex (Diskussion) 19:40, 27. Okt. 2016 (CEST)
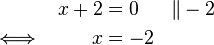
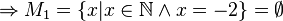 (da
(da 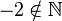 )
)
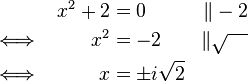
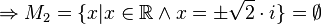 (da
(da 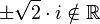 )
)
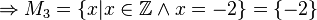 (da
(da 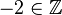 )
)
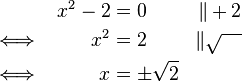
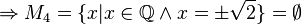 (da
(da 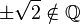 )
)
 (da
(da 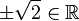 )
)
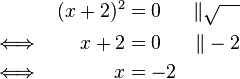
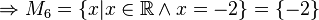 (da
(da 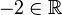 )
)