Elementare Funktionen: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Test) |
(→Sinus und Kosinus am Einheitskreis) |
||
| Zeile 36: | Zeile 36: | ||
==Sinus und Kosinus im rechtwinkligen Dreieck== | ==Sinus und Kosinus im rechtwinkligen Dreieck== | ||
==Sinus und Kosinus am Einheitskreis== | ==Sinus und Kosinus am Einheitskreis== | ||
| + | <iframe scrolling="no" src="https://www.geogebra.org/material/iframe/id/D7XvfBPZ/width/1901/height/1504/border/888888/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="1901px" height="1504px" style="border:0px;"> </iframe> | ||
| + | |||
==Graphen der Funktionen sin und cos== | ==Graphen der Funktionen sin und cos== | ||
==Spezielle Funktionswerte== | ==Spezielle Funktionswerte== | ||
Version vom 16. Februar 2017, 10:41 Uhr
Inhaltsverzeichnis |
Test
Der Funktionsbegriff
Elemente der Mengenlehre
Kreuzprodukt zweier Mengen
Es seien M und N zwei nicht leere Mengen.
Unter dem Kreuzprodukt MxN versteht man die mnge aller geordenten Paare (a,b) mit a aus M und b aus N.
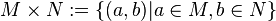
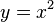
Relationen
Ordnungsrelationen
Äquivalenzrelationen
Funktionen als spezielle Relationen
Linkstotal
Rechtseindeutig
Eineindeutige Funktionen
Umkehrfunktion
Lineare Funktionen
proportionale Funktionen
nichtproportionale lineare Funktionen
Anstieg bei zueinander senkrechten Funktionsgraphen
ax+by+c=0
quadratische Funktionen
Parabeln
Parabel als Ortskurve
Parabel als Funktion
Scheitelpunktslage
auf x-Achse verschoben
mit beliebigem Vektor verschoben
Winkelfunktionen
Sinus und Kosinus im rechtwinkligen Dreieck
Sinus und Kosinus am Einheitskreis
[ www.geogebra.org is not an authorized iframe site ]

