Elementare Funktionen: Unterschied zwischen den Versionen
AlanTu (Diskussion | Beiträge) K (→Steigung) |
AlanTu (Diskussion | Beiträge) (→Funktionen als spezielle Relationen) |
||
| Zeile 41: | Zeile 41: | ||
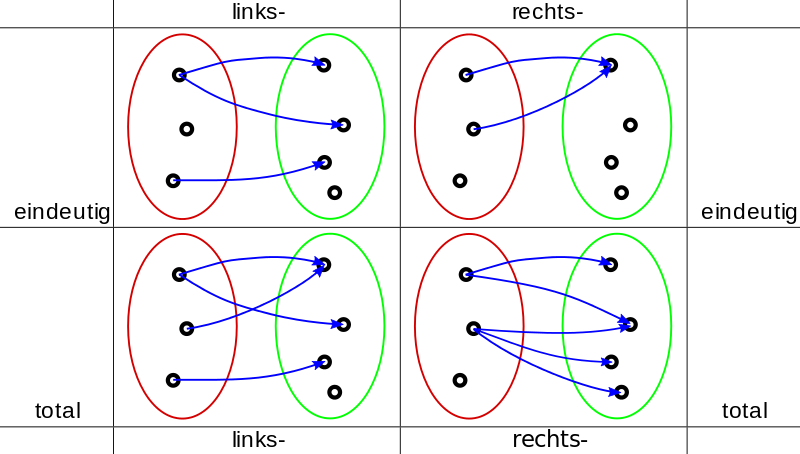
==Funktionen als spezielle Relationen== | ==Funktionen als spezielle Relationen== | ||
| + | [[Datei:Links-rechts eindeutig-total.svg|800px]] | ||
===Linkstotal=== | ===Linkstotal=== | ||
| + | <math>\forall a\in A : \exists b\in B : (a,b)\in R</math> | ||
===Rechtseindeutig=== | ===Rechtseindeutig=== | ||
| + | <math>\forall a\in A : \forall b_1,b_2\in B : (a,b_1)\in R \wedge (a,b_2) \in R \Rightarrow b_1 = b_2</math> | ||
===Eineindeutige Funktionen=== | ===Eineindeutige Funktionen=== | ||
===Umkehrfunktion=== | ===Umkehrfunktion=== | ||
| + | |||
=Lineare Funktionen= | =Lineare Funktionen= | ||
==proportionale Funktionen== | ==proportionale Funktionen== | ||
Version vom 10. April 2017, 22:51 Uhr
Inhaltsverzeichnis |
Die Idee zur Prüfungsvorbereitung: Umstrukturieren des Bekannten
Beispiel: Quadratische Funktion / Schräger Wurf
Eingangsgrößen
| Abwurfhöhe | 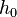
|
| Abwurfgeschwindigkeit (Betrag) | 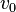
|
| Abwurfwinkel | 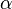
|
Herleitung der Vektorgleichung
x-Komponente
Die Bewegung in x-Richtung wird nur durch den entsprechenden Anteil der Anfangsgeschwindigkeit bewirkt:
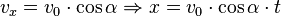
y-Komponente
Es addieren sich:
- y-Komponente der Anfangsgeschwindigkeit:
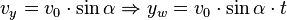
- Fallbewegung nach unten:
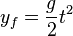
- Damit
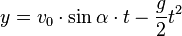
- Ortsvektor der Punktmasse in Abhängigkeit der Zeit:
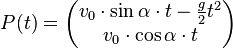
Experimentierumgebung
[ www.geogebra.org is not an authorized iframe site ]
Experimentieraufgaben
Die Punktmasse P möge bei gegebener Abwurfhöhe 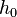 bei
bei 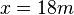 auftreffen. Es gibt hierfür genau zwei Lösungen, welche?
auftreffen. Es gibt hierfür genau zwei Lösungen, welche?
Umstrukturierung
Bekannterweise ist der Graph der Vektorfunktion (I) 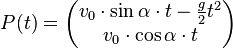 eine Parabel mit der Funktionsgleichung (II)
eine Parabel mit der Funktionsgleichung (II) 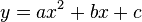 . Entwickeln Sie aus der Vektorfunktion (I) die in der Schule übliche Gleichung (II).
. Entwickeln Sie aus der Vektorfunktion (I) die in der Schule übliche Gleichung (II).
Der Funktionsbegriff
Elemente der Mengenlehre
Kreuzprodukt zweier Mengen
Es seien M und N zwei nicht leere Mengen.
Unter dem Kreuzprodukt MxN versteht man die mnge aller geordenten Paare (a,b) mit a aus M und b aus N.
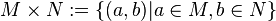
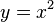
Relationen
Ordnungsrelationen
Äquivalenzrelationen
Funktionen als spezielle Relationen
Linkstotal
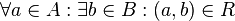
Rechtseindeutig
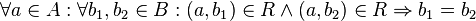
Eineindeutige Funktionen
Umkehrfunktion
Lineare Funktionen
proportionale Funktionen
nichtproportionale lineare Funktionen
Steigung
[ www.geogebra.org is not an authorized iframe site ]
- Das Verhältnis der beiden Katheten eines beliebigen Steigungsdreieck ein und derselben linearen Funktion ist immer gleich.
- Jedes Steigungsdreick ist ein rechtwinkliges Dreieck.
Satz: Durch zwei beliebige voneinander verschiedene Punkte 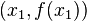 und
und 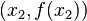 wird eindeutig die Gleichung einer linearen Funktion bestimmt.
wird eindeutig die Gleichung einer linearen Funktion bestimmt.
mehr folgt in Kürze, ich muss erst herausfinden, wie ich die ganzen Herleitungen darstellen kann mit Wiki. Frage: Wie schreibt man Brüche?! Bei mir wird mit "\frac" immer eine Fehlermeldung angezeigt.
Nach \frac braucht man zwei paar geschweifter Klammern (je eins für Zähler und Nenner), dann müsste es funktionieren:
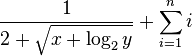
Anstieg bei zueinander senkrechten Funktionsgraphen
ax+by+c=0
quadratische Funktionen
Parabeln
Parabel als Ortskurve
Parabel als Funktion
Scheitelpunktslage
auf x-Achse verschoben
mit beliebigem Vektor verschoben
Winkelfunktionen
Sinus und Kosinus im rechtwinkligen Dreieck
Sinus und Kosinus am Einheitskreis
[ www.geogebra.org is not an authorized iframe site ]