Lösung von Aufgabe 2.04 SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=90%| style="backgro…“) |
*m.g.* (Diskussion | Beiträge) (→Kommentar --*m.g.* (Diskussion) 12:07, 7. Mai 2017 (CEST)) |
||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{|width=90%| style="background-color:#FFFF99; padding:1em" | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| valign="top" | | | valign="top" | | ||
| + | |||
| + | Die folgende Definition ist nicht korrekt. Ändern Sie den Text der Definition so, dass eine korrekte Definition des Begriffs Kreissehne entsteht. | ||
| + | {{Definition|1= Wenn eine Strecke <math>\overline{AB}</math> eine Sehne des Kreises <math>k</math> ist, dann gilt <math>A \in k \land B \in k</math>.}} | ||
| + | ==Lösung 1== | ||
| + | Der Begriff "Sehne" soll hier definiert werden. Also kann man den Begriff nicht für seine eigene Definition verwenden. | ||
| + | |||
| + | ==Kommentar --[[Benutzer:*m.g.*|*m.g.*]] ([[Benutzer Diskussion:*m.g.*|Diskussion]]) 12:07, 7. Mai 2017 (CEST)== | ||
| + | Kann man so sagen. Machen Sie sich in jedem Fall, die Struktur einer Konventionaldefinition deutlich. | ||
| + | {{Definition|1= Wenn <br /> | ||
| + | die Endpunkte <math>A</math> und <math>B</math> der Strecke <math>\overline{AB}</math> auf dem Kreis <math>k</math> liegen, <br /> | ||
| + | dann <br /> | ||
| + | heißt <math>\overline{AB}</math> Sehne von <math>k</math>.}} | ||
| + | Definierende Eigenschaft: <br /> | ||
| + | :Endpunkte der Strecke liegen auf dem Kreis. | ||
| + | zu definierender Begriff:<br /> | ||
| + | : Kreissehne<br /> | ||
| + | Grundlegende Struktur der Definition: | ||
| + | {{Definition|1= Wenn <br /> | ||
| + | ''definiernde Eigenschaft'', <br /> | ||
| + | dann <br /> | ||
| + | ''zu definierender Begriff''.}} | ||
| + | |||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 7. Mai 2017, 11:09 Uhr
|
Die folgende Definition ist nicht korrekt. Ändern Sie den Text der Definition so, dass eine korrekte Definition des Begriffs Kreissehne entsteht. Definition Wenn eine Strecke Lösung 1Der Begriff "Sehne" soll hier definiert werden. Also kann man den Begriff nicht für seine eigene Definition verwenden. Kommentar --*m.g.* (Diskussion) 12:07, 7. Mai 2017 (CEST)Kann man so sagen. Machen Sie sich in jedem Fall, die Struktur einer Konventionaldefinition deutlich. Definition Wenn die Endpunkte dann heißt Definierende Eigenschaft:
zu definierender Begriff:
Grundlegende Struktur der Definition: Definition Wenn definiernde Eigenschaft, dann zu definierender Begriff. |
eine Sehne des Kreises 
ist, dann gilt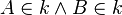 
.
und 
der Strecke 
