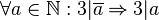|
|
| Zeile 3: |
Zeile 3: |
| | | valign="top" | | | | valign="top" | |
| | | | |
| − | =Mathematische Aussagen= | + | =Implikationen= |
| | ==Beispiele== | | ==Beispiele== |
| − | ===Primzahlen=== | + | ===Teilbarkeit durch 3=== |
| − | Es lassen sich z.B. die folgenden Aussagen zu Primzahlen machen:
| + | :Wenn die Quersumme <math>\overline{a}</math>einer natürlichen Zahl <math>a</math> durch <math>3</math> teilbar ist, dann ist auch die Zahl <math>a</math> durch <math>3</math> teilbar.<br /> |
| − | {| class="wikitable"
| + | :In Formelsprache: <math>\forall a \in \mathbb{N}: 3|\overline{a} \Rightarrow 3|a</math> |
| − | |-
| + | |
| − | ! Aussage!! Wahrheitswert
| + | |
| − | |-
| + | |
| − | | Die Zahl <math>3</math> ist eine Primzahl.|| wahr
| + | |
| − | |-
| + | |
| − | | Die Zahl <math>4</math> ist eine Primzahl.|| falsch
| + | |
| − | |-
| + | |
| − | | Es gibt unendlich viele Primzahlen.|| wahr
| + | |
| − | |-
| + | |
| − | | Es gibt genauso viele Primzahlen wie es natürliche Zahlen gibt.|| wahr.
| + | |
| − | |}
| + | |
| − | Keine Aussage zu Primzahlen ist:<br />
| + | |
| − | : Jede natürlich Zahl, die nur durch sich selbst und durch 1 teilbar ist, heißt Primzahl.
| + | |
| − | | + | |
| − | ===Wichtige Sätze der Schulgeometrie===
| + | |
| − | Sätze sind Aussagen, die wahr sind. Eine Aussage, die nicht wahr ist, kann demzufolge auch kein Satz sein.
| + | |
| − | *Innenwinkelsatz für Dreiecke: Die Innenwinkelsumme eines jeden Dreiecks ist gleich der Größe eines gestreckten Winkels.
| + | |
| − | *Satz des Pythagoras: In rechtwinkligen Dreiecken ist die Summe der Quadrate der Katheten gleich dem Quadrat der Hypotenuse.
| + | |
| − | *Starker Außenwinkelsatz: Jeder Außenwinkel eines Dreiecks ist so groß wie die Summe der beiden nichtanliegenden Innenwinkel des Dreiecks.
| + | |
| − | *Basiswinkelsatz: Wenn ein Dreieck gleichschenklig ist, dann sind seine Basiswinkel kongruent zueinander.
| + | |
| − | Ergänzen Sie durch eigene Sätze, die Sie noch aus der Schule kennen:
| + | |
| − | * .....
| + | |
| − | * .....
| + | |
| − | * .....
| + | |
| − | | + | |
| − | ==Begriff der Aussage==
| + | |
| − | Ein sauber Definition des Begriffs mathematische Aussage bleibt uns hier versagt, es reichen intuitive Vorstellungen der folgenden Art:
| + | |
| − | | + | |
| − | *Eine Aussage ist ein sprachliches Gebilde, welche zur Beschreibung und Mitteilung von Sachverhalten dienen. (Kleine Enzyklopädie Mathematik. VEB Bibliographisches Institut Leipzig)(1983).
| + | |
| − | | + | |
| − | Bei einer mathematischen Aussage setzt man zwei Prinzipien voraus:
| + | |
| − | | + | |
| − | *Das Prinzip vom ausgeschlossenen Dritten: Eine Aussage ist wahr (1) oder falsch (0).
| + | |
| − | *Das Prinzip vom ausgeschlossenen Widerspruch: Eine Aussage kann nicht gleichzeitig wahr und falsch sein.
| + | |
| − | | + | |
| − | Beide Prinzipien zusammengefasst:
| + | |
| − | *Eine mathematische Aussage ist entweder wahr oder falsch.
| + | |
| − | | + | |
| − | ==Weitere Beispiele und Gegenbeispiele für Aussagen==
| + | |
| − | Ergänzen Sie die folgende Tabelle:
| + | |
| − | {| class="wikitable"
| + | |
| − | |-
| + | |
| − | ! keine Aussage!! Aussage
| + | |
| − | |-
| + | |
| − | | Gründonnerstag|| Gründonnerstag regnet es immer.
| + | |
| − | |-
| + | |
| − | | Ab jetzt heißt Raider Twix.|| Im Januar hat man festgelegt, dass Raider Twix heißt.
| + | |
| − | |-
| + | |
| − | | Die Quadratwurzel aus einer negativen Zahl ziehen.|| Die Quadratwurzel aus einer nagativen Zahl in in <math>\mathbb{R}</math> nicht definiert.
| + | |
| − | |-
| + | |
| − | | Konstruiere einen Kreis.|| ihr Beispiel
| + | |
| − | |-
| + | |
| − | | ihr Beispiel || ihr Beispiel
| + | |
| − | |}
| + | |
| − | | + | |
| − | ==Die Negation einer Aussage==
| + | |
| − | ===Beispiele===
| + | |
| − | {| class="wikitable"
| + | |
| − | |-
| + | |
| − | ! Aussage !! Negation der Aussage
| + | |
| − | |-
| + | |
| − | | <math>2</math> ist Primzahl|| <math>2</math> ist keine Primzahl
| + | |
| − | |-
| + | |
| − | | Die Eisernen steigen auf.|| Die Eisernen steigen nicht auf.
| + | |
| − | |-
| + | |
| − | | Die Hose ist grün.|| Die Hose ist nicht grün.
| + | |
| − | |-
| + | |
| − | | Bier schmeckt gut. || Bier schmeckt nicht gut.
| + | |
| − | |-
| + | |
| − | | ihr Beispiel || ihr Beispiel
| + | |
| − | |}
| + | |
| − | | + | |
| − | ===Wahrheitswerttabelle===
| + | |
| − | Wenn <math>p</math> eine Aussage ist, dann ist es üblich, mit <math>\neg p</math> die Negation von <math>p</math> zu kennzeichnen.
| + | |
| − | {| class="wikitable"
| + | |
| − | |-
| + | |
| − | ! <math>p</math> !! <math>\neg p</math>
| + | |
| − | |-
| + | |
| − | | wahr || falsch
| + | |
| − | |-
| + | |
| − | | falsch|| wahr
| + | |
| − | |}
| + | |
| − | Hinweis: Die LaTex-Syntax für das Zeichen <math>\neg</math> ist \neg.
| + | |
| − | ==Verknüpfung zweier Aussagen==
| + | |
| − | ===Das logische und===
| + | |
| − | ==== Die Idee====
| + | |
| − | Zwei Aussagen <math>a</math> und <math>b</math> lassen sich durch ein logisches und zu einer Aussage zusammenfassen.
| + | |
| − | ==== Beispiel Teilbarkeit von Summen====
| + | |
| − | Wenn <math>t|a</math> und <math>t|b</math>, dann <math>t|(a+b)</math>.<br />
| + | |
| − | Voraussetzung <math>1</math>: <math>t|a</math><br />
| + | |
| − | Voraussetzung <math>2</math>: <math>t|b</math><br />
| + | |
| − | Zusammenfassung zu einer Voraussetzung: <math>t|a \land t|b</math>.
| + | |
| − | ====Wahrheitswertabelle====
| + | |
| − | {| class="wikitable" | + | |
| − | |-
| + | |
| − | ! <math>a</math> !! <math>b</math> !! <math>a \land b</math>
| + | |
| − | |-
| + | |
| − | | wahr || wahr || wahr
| + | |
| − | |-
| + | |
| − | | wahr || falsch|| falsch
| + | |
| − | |-
| + | |
| − | | falsch || wahr|| falsch
| + | |
| − | |-
| + | |
| − | | falsch || falsch || falsch
| + | |
| − | |}
| + | |
| − | | + | |
| − | Die Verknüpfung zweier Aussagen durch ein logisches und ist genau dann wahr, wenn beide Aussagen wahr sind.
| + | |
| − | ==Das logische oder==
| + | |
| − | ===Die Idee===
| + | |
| − | Zwei Aussagen lassen sich durch ein logisches oder zu einer Aussage zusammenfassen.
| + | |
| − | ===Wahrheitswerttabelle===
| + | |
| − | {| class="wikitable" | + | |
| − | |-
| + | |
| − | ! <math>a</math> !! <math>b</math> !! <math>a \lor b</math>
| + | |
| − | |- | + | |
| − | | wahr || wahr || wahr
| + | |
| − | |-
| + | |
| − | | wahr || falsch|| wahr
| + | |
| − | |-
| + | |
| − | | falsch || wahr || wahr
| + | |
| − | |-
| + | |
| − | | falsch || falsch || falsch
| + | |
| − | |}
| + | |
| − | Die Verknüpfung zweier Aussagen ist genau dann falsch, wenn beide Aussagen falsch sind.<br />
| + | |
| − | Hinweis: Das logische oder entspricht nicht dem allgemeinen Sprachgebrauch in der Umgangsprache. Umgangssprachlich ist das oder ein entweder oder (exklusives oder).
| + | |
| − | ===Wahrheitswerttabelle entweder oder===
| + | |
| − | exklusives oder
| + | |
| − | {| class="wikitable"
| + | |
| − | |-
| + | |
| − | ! <math>a</math> !! <math>b</math> !! <math>a \dot\lor b</math>
| + | |
| − | |-
| + | |
| − | | wahr || wahr || falsch
| + | |
| − | |-
| + | |
| − | | wahr || falsch|| wahr
| + | |
| − | |-
| + | |
| − | | falsch || wahr || wahr
| + | |
| − | |-
| + | |
| − | | falsch || falsch || falsch
| + | |
| − | |}
| + | |
| | | | |
| | | | |
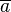 einer natürlichen Zahl
einer natürlichen Zahl  durch
durch  teilbar ist, dann ist auch die Zahl
teilbar ist, dann ist auch die Zahl