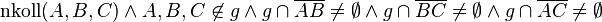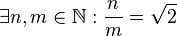Implikationen SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Implikation 5: Nonsens) |
||
| (34 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
| valign="top" | | | valign="top" | | ||
| − | = | + | =Implikationen= |
| + | ==Generelle Kennzeichnung von Implikationen== | ||
| + | Implikationen sind spezielle mathematische Aussagen, deren Typ sich kurz wie folgt darstellen bzw. beschreiben lässt: | ||
| + | * Wenn <math>a</math> dann <math>b</math>. | ||
| + | * Aus <math>a</math> folgt <math>b</math>. | ||
| + | * <math>a</math> impliziert <math>b</math>. | ||
| + | * <math>b</math> ist eine Folgerung aus <math>a</math>. | ||
| + | * Unter der Voraussetzung, dass <math>a</math> gilt, gilt auch <math>b</math>. | ||
| + | * <math>a</math> ist hinreichend dafür, dass <math>b</math> gilt. | ||
| + | * <math>a \Rightarrow b</math> | ||
| + | |||
| + | Die Aussage <math>a</math> heißt in der Implikation <math>a \Rightarrow b</math> Voraussetzung, die Aussage <math>b</math> wird Behauptung genannt. | ||
| + | |||
==Beispiele== | ==Beispiele== | ||
| − | === | + | ===Implikation 1: Satz zur Teilbarkeit durch 3=== |
| − | + | :Wenn die Quersumme <math>\overline{a}</math>einer natürlichen Zahl <math>a</math> durch <math>3</math> teilbar ist, dann ist auch die Zahl <math>a</math> durch <math>3</math> teilbar.<br /> | |
| − | { | + | :In Formelsprache: <math>\forall a \in \mathbb{N}: 3|\overline{a} \Rightarrow 3|a</math> |
| − | + | *Voraussetzung: <math>3|\overline{a}</math> | |
| − | + | *Behauptung: <math>3|a</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | * | + | |
| − | * | + | |
| + | === Implikation 2: Satz zur Teilbarkeit von Summen=== | ||
| + | :Für alle natürlichen Zahlen <math>a,b,t</math> gilt:<br /> | ||
| + | ::Wenn <math>t</math> die Zahlen <math>a</math> und <math>b</math> teilt, dann teilt <math>t</math> auch die Summe <math>a+b</math>. | ||
| + | :In Formelsprache: | ||
| + | :<math>\forall a,b,t \in \mathbb{N}:</math><br /> | ||
| + | ::<math>t|a \land t|b \Rightarrow t|(a+b)</math> | ||
| + | *Voraussetzung: Wir haben zwei Voraussetzungen die durch das logische und zu einer Voraussetzung zusammengefasst werden: | ||
| + | ::V<sub>1</sub>: <math>t|a</math> | ||
| + | ::V<sub>2</sub>: <math>t|b</math> | ||
| + | ::V: <math>t|a \land t|b</math> | ||
| + | *Behauptung:<br /> | ||
| + | ::<math>t|(a+b)</math> | ||
| + | ===Implikation 3: Nebenwinkelsatz=== | ||
| + | :Wenn <math>\alpha</math> und <math>\beta</math> Nebenwinkel sind, dann ist die Summe ihrer Größen <math>180^\circ</math> | ||
| + | In anderer Formulierung ohne wenn-dann: | ||
| + | :Nebenwinkel ergänzen sich zu <math>180^\circ</math> | ||
| + | *Voraussetzung: | ||
| + | :: <math>\alpha</math> und <math>\beta</math> sind Nebenwinkel | ||
| + | *Behauptung: | ||
| + | ::<math>\alpha</math> und <math>\beta</math> sind supplementär. | ||
| + | ===Implikation 4: Scheitelwinkelsatz=== | ||
| + | :Wenn die beiden Winkel <math>\alpha</math> und <math>\beta</math> Scheitelwinkel sind, dann haben sie dieselbe Größe. | ||
| + | alternative Formulierung ohne wenn-dann: | ||
| + | :Scheitelwinkel haben dieselbe Größe. oder | ||
| + | :Scheitelwinkel sind kongruent zueinander. | ||
| + | *Voraussetzung | ||
| + | ::<math>\alpha</math> und <math>\beta</math> sind Scheitelwinkel | ||
| + | *Behauptung | ||
| + | ::<math>|\alpha|=|\beta|</math> bzw. <math>\alpha \cong \beta</math> | ||
| + | ===Implikation 5: Nonsens=== | ||
| + | :Wenn die Gerade <math>g</math> durch keinen der Eckpunkte des Dreiecks <math>\overline{ABC}</math> geht und jede der drei Seiten <math>\overline{AB}, \overline{BC}, \overline{AC}</math> geht, dann ist <math>\sqrt{2}</math> eine rationale Zahl. | ||
| + | *Voraussetzung: | ||
| + | :<math>\text{nkoll}(A,B,C) \land A,B,C \not\in g \land g \cap \overline{AB} \not= \empty \land g \cap \overline{BC} \not= \empty \land g \cap \overline{AC} \not= \empty</math> | ||
| + | *Behauptung: | ||
| + | :<math>\exist n,m \in \mathbb{N}: \frac{n}{m} = \sqrt{2}</math> | ||
| + | ===Implikation 6: Satz des Thales=== | ||
| + | {{#ev:youtube|yOgu9FAK5AM}} | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
Aktuelle Version vom 10. Mai 2017, 17:04 Uhr
ImplikationenGenerelle Kennzeichnung von ImplikationenImplikationen sind spezielle mathematische Aussagen, deren Typ sich kurz wie folgt darstellen bzw. beschreiben lässt:
Die Aussage BeispieleImplikation 1: Satz zur Teilbarkeit durch 3
Implikation 2: Satz zur Teilbarkeit von Summen
Implikation 3: Nebenwinkelsatz
In anderer Formulierung ohne wenn-dann:
Implikation 4: Scheitelwinkelsatz
alternative Formulierung ohne wenn-dann:
Implikation 5: Nonsens
Implikation 6: Satz des Thales |
 dann
dann  .
.

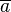 einer natürlichen Zahl
einer natürlichen Zahl  teilbar ist, dann ist auch die Zahl
teilbar ist, dann ist auch die Zahl 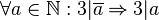
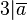
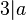
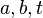 gilt:
gilt: die Zahlen
die Zahlen 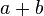 .
.
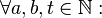
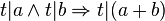
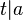
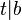
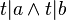
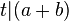
 und
und  Nebenwinkel sind, dann ist die Summe ihrer Größen
Nebenwinkel sind, dann ist die Summe ihrer Größen 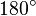
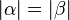 bzw.
bzw. 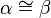
 durch keinen der Eckpunkte des Dreiecks
durch keinen der Eckpunkte des Dreiecks  geht und jede der drei Seiten
geht und jede der drei Seiten 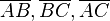 geht, dann ist
geht, dann ist 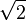 eine rationale Zahl.
eine rationale Zahl.