Untergruppen SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Untergruppenkriterium 1) |
*m.g.* (Diskussion | Beiträge) (→Untergruppenkriterium 2) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 21: | Zeile 21: | ||
# <math>\forall a,b \in U: a \odot b \in U</math>, | # <math>\forall a,b \in U: a \odot b \in U</math>, | ||
# <math>\forall a \in U: a^{-1} \in U</math>. | # <math>\forall a \in U: a^{-1} \in U</math>. | ||
| + | Beweis: Übungsaufgabe | ||
| + | |||
==Untergruppenkriterium 2== | ==Untergruppenkriterium 2== | ||
'''Satz 3: (2. Untergruppenkriterium)''' | '''Satz 3: (2. Untergruppenkriterium)''' | ||
| Zeile 27: | Zeile 29: | ||
:<math>[U,\odot]</math> ist genau dann Untergruppe von <math>[G,\odot]</math>, wenn | :<math>[U,\odot]</math> ist genau dann Untergruppe von <math>[G,\odot]</math>, wenn | ||
* <math>\forall a, b \in U: a \odot b^{-1} \in U </math>. | * <math>\forall a, b \in U: a \odot b^{-1} \in U </math>. | ||
| + | Beweis: Übungsaufgabe | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Algebra]] | [[Kategorie:Algebra]] | ||
Aktuelle Version vom 14. Mai 2017, 16:50 Uhr
UntergruppenBeispiele
DefinitionDefinition 6: (Untergruppe)
Untergruppenkriterium 1Satz 2: (1. Untergruppenkriterium)
Beweis: Übungsaufgabe Untergruppenkriterium 2Satz 3: (2. Untergruppenkriterium)
Beweis: Übungsaufgabe |
![[\mathbb{Z}|_2, +]](/images/math/b/f/a/bfac4357e3f1dc2a83e6dd4dd6349274.png) ist eine Untergruppe von
ist eine Untergruppe von ![[\mathbb{Z}, +]](/images/math/8/2/8/828d3197747f0dc881f51c684f1a4c7d.png)
![[G,\odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe und
eine Gruppe und 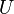 eine Teilmenge von
eine Teilmenge von  .
.![[U,\odot]](/images/math/a/c/c/accc85078e0a1b7e699636b07b93c89b.png) selbst eine Gruppe ist, dann ist
selbst eine Gruppe ist, dann ist 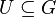 mit
mit 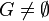 .
.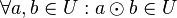 ,
,
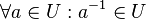 .
.
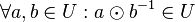 .
.

