Benutzer:Jaschkamc: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „miniatur Wie Groß ist der Flächeninhalt des Quadrates <math>Qges</math> ohne die Löcher? Diese Frage stellte ich meinem 21 M…“) |
|||
| Zeile 5: | Zeile 5: | ||
Diese Frage stellte ich meinem 21 Monate alten Sohn. Er soll ja wissen womit er spielt. | Diese Frage stellte ich meinem 21 Monate alten Sohn. Er soll ja wissen womit er spielt. | ||
| − | <math> | + | <math>A_ges= Q-(Tr+Ra+Kr)</math> |
<math>Q= Quadrat</math> | <math>Q= Quadrat</math> | ||
| Zeile 25: | Zeile 25: | ||
<math>r</math>= Radius | <math>r</math>= Radius | ||
| − | <math> | + | <math>A_ges= a^2 - ((1/2*(a+c)*h) + (1/2*d1*d2) + (\pi*r^2)</math> |
| + | |||
| + | Hallo Jaschkamc,<br/> | ||
| + | das ist ein tolles Spiel um Kindern Geometrie näher zu bringen, sehr schön ;) | ||
| + | Bestimmt hast du in der Didaktik der Mathematik das ''van Hiele'' Modell kennengelernt. Dein Spielwürfel würde hier die Niveaustufe 0 ''Räumlich-anschauungsgebundenes Denken (Visualization)'' darstellen. | ||
| + | Sprich geometrische Objekte als einprägsames Ganzes, als Phänomen wahrnehmen und andere demnach beispielhaft zuordnen. <br/> | ||
| + | Deine Formeln und Anmerkungen sind korrekt. Hast du vllt. für uns Längen, mit denen wir rechnen können?<br/> | ||
| + | Lieber Gruß --[[Benutzer:Tutor: Alex|Tutor: Alex]] ([[Benutzer Diskussion:Tutor: Alex|Diskussion]]) 21:59, 30. Mai 2017 (CEST) | ||
Version vom 30. Mai 2017, 20:59 Uhr
Wie Groß ist der Flächeninhalt des Quadrates 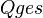 ohne die Löcher?
ohne die Löcher?
Diese Frage stellte ich meinem 21 Monate alten Sohn. Er soll ja wissen womit er spielt.
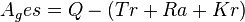
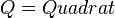
 = Seitenlänge
= Seitenlänge
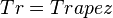
 und
und  = zueinander parallele Seiten
= zueinander parallele Seiten
 = rechtwinklig zu
= rechtwinklig zu  und
und 
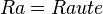
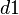 und
und 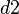 = Diagonalen
= Diagonalen
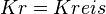
 = Radius
= Radius
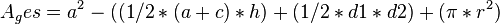
Hallo Jaschkamc,
das ist ein tolles Spiel um Kindern Geometrie näher zu bringen, sehr schön ;) Bestimmt hast du in der Didaktik der Mathematik das van Hiele Modell kennengelernt. Dein Spielwürfel würde hier die Niveaustufe 0 Räumlich-anschauungsgebundenes Denken (Visualization) darstellen. Sprich geometrische Objekte als einprägsames Ganzes, als Phänomen wahrnehmen und andere demnach beispielhaft zuordnen.
Deine Formeln und Anmerkungen sind korrekt. Hast du vllt. für uns Längen, mit denen wir rechnen können?
Lieber Gruß --Tutor: Alex (Diskussion) 21:59, 30. Mai 2017 (CEST)


