Lösung von Aufgabe 1.1 (SoSe 17): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 17: | Zeile 17: | ||
Es sei <math> m=2*n^2 </math> , somit gilt: <math> k^2 = 2*m </math> , wobei auch <math> m \in \mathbb{N}</math> .<br/> | Es sei <math> m=2*n^2 </math> , somit gilt: <math> k^2 = 2*m </math> , wobei auch <math> m \in \mathbb{N}</math> .<br/> | ||
Wie du schon richtig erkannt hast, sind die Quadrate ungerader Zahlen wieder ungerade, kannst du das auf <math> l </math> anwenden? (geht so ähnlich wie oben)<br/> | Wie du schon richtig erkannt hast, sind die Quadrate ungerader Zahlen wieder ungerade, kannst du das auf <math> l </math> anwenden? (geht so ähnlich wie oben)<br/> | ||
| − | So ist also die Menge der natürlichen Zahlen, deren Quadrate gerade sind <math> B = \{2,4,6,...\}=\{x | + | So ist also die Menge der natürlichen Zahlen, deren Quadrate gerade sind <math> B = \{2,4,6,...\}=\{x\vert x^2 \ ist \ gerade \wedge x \in \mathbb{N}\} </math> . |
Somit gilt für die Mengen <math> A=B </math> <br><br/> | Somit gilt für die Mengen <math> A=B </math> <br><br/> | ||
--[[Benutzer:Tutor: Alex|Tutor: Alex]] ([[Benutzer Diskussion:Tutor: Alex|Diskussion]]) 16:43, 31. Mai 2017 (CEST) | --[[Benutzer:Tutor: Alex|Tutor: Alex]] ([[Benutzer Diskussion:Tutor: Alex|Diskussion]]) 16:43, 31. Mai 2017 (CEST) | ||
Aktuelle Version vom 31. Mai 2017, 17:25 Uhr
Es sei A die Menge der geraden natürlichen Zahlen, B die Menge der natürlichen Zahlen, deren Quadrate gerade ist. Vergleichen Sie die Mengen.
Ich habe folgende Hypothese aufgestellt, weiß allerdings noch nicht, wie ich sie mathematisch umformuliere:
Ich bezeichne als n die ungeraden Zahlen und damit als n+1 die geraden.
A: n+1
B: b²= n+1 (b könnte n oder n+1 sein-> also gerade ungerade) Aber: habe festgestellt, dass jede Zahl die ungerade ist, auch deren Quadrat ungerade ist und jede Zahl, die gerade ist, auch deren Quadrat gerade ist) -> somit wäre für mich b nur n+1
Also wären A und B gleiche Mengen -> A=B
Hallo Kissa052,
deine Schlussfolgerung, dassist, ist vollkommen richtig, jetzt müssen wir das nur noch mathematisch aufschreiben. Schreibe für eine gerade Zahl
und für eine ungerade Zahl
mit
.
Die Menge der geraden natürlichen Zahlen ist dann also. (bei der Null können wir uns streiten ;P )
Quadriert man eine gerade Zahl, so erhält man wieder eine gerade Zahl, das kann man so zeigen:. Es sei
, somit gilt:
, wobei auch
.
Wie du schon richtig erkannt hast, sind die Quadrate ungerader Zahlen wieder ungerade, kannst du das aufanwenden? (geht so ähnlich wie oben)
So ist also die Menge der natürlichen Zahlen, deren Quadrate gerade sind. Somit gilt für die Mengen
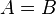
--Tutor: Alex (Diskussion) 16:43, 31. Mai 2017 (CEST)

