Pfeilklassen SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „=Aufgabe 1 (Pfeilklassen SoSe 2017)= In einem kartesischen Koordinatensystem mit dem Ursprung <math>O</math> seien die Punkte <math>P\left(\frac{1}{2}\sqrt{2},…“) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2 (Pfeilklassen SoSe 2017)) |
||
| Zeile 4: | Zeile 4: | ||
=Aufgabe 2 (Pfeilklassen SoSe 2017)= | =Aufgabe 2 (Pfeilklassen SoSe 2017)= | ||
Es sei <math>\overline{ABC}</math> ein rechtwinkliges Dreieck mit dem rechten Winkel bei <math>C</math>.<math>q</math>seien wie üblich die Längen der Hypotenusenabschnitte von <math>\overline{ABC}</math>. Bestimmen Sie die Koordinaten der Pfeilklassen <math>\overrightarrow{AC}, \overrightarrow{AB}</math> und <math>\overrightarrow{BC}</math> bezüglich eines Koordinatensystems, dessen Ursprung der Fußpunkt der Höhe <math>h_c</math> ist. Ferner gelte, dass <math>B</math> auf der positiven <math>x-</math>Achse und <math>C</math> auf der positiven <math>y-</math>Achse liegt. | Es sei <math>\overline{ABC}</math> ein rechtwinkliges Dreieck mit dem rechten Winkel bei <math>C</math>.<math>q</math>seien wie üblich die Längen der Hypotenusenabschnitte von <math>\overline{ABC}</math>. Bestimmen Sie die Koordinaten der Pfeilklassen <math>\overrightarrow{AC}, \overrightarrow{AB}</math> und <math>\overrightarrow{BC}</math> bezüglich eines Koordinatensystems, dessen Ursprung der Fußpunkt der Höhe <math>h_c</math> ist. Ferner gelte, dass <math>B</math> auf der positiven <math>x-</math>Achse und <math>C</math> auf der positiven <math>y-</math>Achse liegt. | ||
| + | =Aufgabe 3 (Pfeilklassen SoSe 2017)= | ||
| + | Es sei <math>\overline{ABCD}</math> ein Parallelogramm. Beweisen Sie: <math>\frac{1}{2} \overrightarrow{AB} \oplus \frac{1}{2} \overrightarrow{BC} = \frac{1}{2} \overrightarrow{AD} \oplus \frac{1}{2} \overrightarrow{DC}</math>. | ||
Version vom 4. Juni 2017, 13:41 Uhr
Aufgabe 1 (Pfeilklassen SoSe 2017)
In einem kartesischen Koordinatensystem mit dem Ursprung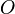 
seien die Punkte 
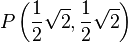und 
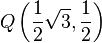gegeben.
Bestimmen Sie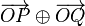 
Berechnen Sie die Länge die jeder Pfeil aus 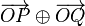hat.
Aufgabe 2 (Pfeilklassen SoSe 2017)
Es sei 
ein rechtwinkliges Dreieck mit dem rechten Winkel bei 
.
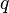seien wie üblich die Längen der Hypotenusenabschnitte von . Bestimmen Sie die Koordinaten der Pfeilklassen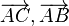 
und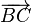 
bezüglich eines Koordinatensystems, dessen Ursprung der Fußpunkt der Höhe 
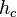ist. Ferner gelte, dass 
auf der positiven 
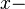Achse und auf der positiven 
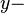Achse liegt.
Aufgabe 3 (Pfeilklassen SoSe 2017)
Es sei 
ein Parallelogramm. Beweisen Sie: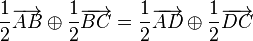 
.
