|
|
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| | + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> |
| | + | {|width=90%| style="background-color:#FFFF99; padding:1em" |
| | + | | valign="top" | |
| | | | |
| | = Halbebenen und das Axiom von Pasch = | | = Halbebenen und das Axiom von Pasch = |
| Zeile 4: |
Zeile 7: |
| | === Analogiebetrachtungen === | | === Analogiebetrachtungen === |
| | | | |
| − | {| class="wikitable center"
| |
| − | | style="background: #DDFFDD;"| <center>'''Halbgeraden'''</center>
| |
| − | | style="background: #DDFFDD;"| <center>'''Halbebenen'''</center>
| |
| | | | |
| − | |-
| |
| − | | <ggb_applet width="398" height="401" version="3.2" ggbBase64="UEsDBBQACAAIAGSMwjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1Vlbb9s2FH5efwUhFMWGIbIoWbKF2imyrg8BsiVdsmIYhgG0RMtcdHElypcW/e87vMiW7FhR3KQXP0TmRYeH3+VQckavVkmMFjQvWJaODWxaBqJpkIUsjcZGyacnQ+PV6bNRRLOITnKCplmeED42HNM2RH/JTp/9MCpm2RKRWE55x+hybExJXFADFfOckrCYUcob/aRcsZiRfH05+Y8GvNgOqCDn6byEVXheQl+QhBesqJo9ueA8ZvxXtmAhzVGcBWPDcyF1+PaO5pwFJB4bfUv12GPD3hmELkeMzrKcfchSLqZvg0+hB6GCfaBwpyX6Rj250REtg5iFjKRiMzIPmITQkoV8BiH9IYSkLJoJgHxfRQuyLA+v1wWnCVr9TfNsbJxg7Auk16o5dEWjgLxgQdeSI/WWDEMX15RzoKVAZEW3gEU5CxuN8+KXLN52zTOW8tdkzstccurormu+FgvAWrlI+CyNYqr7MEA+o8HtJFtdSxCwo0LfrOfyFpnQJHqdxVmOcgGvCxP0daKuco7IdDPLknMsOUPHEEE349i35Qx5nairnBWzVKWmd46rXWOrWoYVSHQIGEGKm83HZEKBWgOVKeMXVQMkcLvdqrjh9zKZgAfqItjExI8Vc9Tbkc/oluYpjZVIUuC2zMoCLYQY1VoykZAGLIGmGtCQEEHXn5CA6g1plNMqceUgBZgctepC3Oke9aokRA4F5BpwKAWwHy72IpzKwSVjIzEj00Ah4aJXWCGmCQWfcKkJKakNNmfGpihk0t+Vk/X4FmUY3lORiyX94kLi+YxAppUJYrIGv9c3JSP+loXNrZIUIJP7ANvNRQBBypzSUNc4rpWM5hBS+qKGuASqQCvIAaocWoNhHRODtz+ou+UkZSJhf7mwqxlWqNyDz9uj8Kn7R2L1tdEZmK5t1T+uAss27f7DwAqyJCFpiFKSwMIX4HeJEBOnACKWUBQiWACnUCl5NRCpUDrAHu6idGxgjYxmNeEzMG1Ki0JktNl073husOuoymXZndm5nE4LygWcnqe1ZreRt4X/xDL9vrzFNp0mEY6CH4jwXG/bjXfraQsC9H2q5hSqqrEEjtyA8Xbq/iDrrsxN2pnLIVKF+eQwcX5n4hoSTkOmDADTL/Vsil5E/CXaEPZEtempCNxFoo1ASUQsrH2ecjikqCz6+2fPLaVzcehfpjc5SQvx8Kfm1M60A0q4khWvqYVoTwRX7SJols2ro8omthV18vqtlM6h6dveEFvW0MMD3xkq52PT83z4OB72nL6NRUU4vowe9OLVHg1Bdy8GX8qL8SEvCvNtrfhZdNa8iE0XC4t5ztDx3AH8kZw45qBO1MDXlPjmwHJs13d8x3Xh9aL//Tjzmkaif0cbV4fqdNiujUJHq6gNv4g+SPvjkdUqCa+bJCzTHdyhCFBK32pIQhXrk4HZdwbeVhLO9yOJdxAzy7ue3GW7IhYqWMVleVgQdpsgmq9btX0eR3rHOnDXSbwWEX31SLsN3WVDtVcuTWxAck4LeAXUO+bQlkcloqu5wPxonvar+uJBPC0ehaf7X10ehaa7yvJanJT7RfwrkAa9OYQWRUvDsjTU1BL10MLYIaB3HzXL74kay/Rs28We7TsYDzB8q8qmPfD7ntvHbt/xh7735gQ/AT3tPFDNw+rH5U93AZ+WCc1ZYGzniyVho2W13f3ddYYU35/fDV1xrHN88b7M+Muzt/9+/PkTUg1jP2MOdxjN25/wPeiR1MKKC3JD/2oeT/qH1wIImFY5qx9hQSaaanvPgapo+0Ndpl3Xb3zqD9D3Q2/vQX/yEOjtzi8oD3/q/VaRd70K+YNQN0CbZFlMwaoVJmTXYTV9dhLxcSC5d/4E46tTpN8C4f0ichoiev5PtqC5qGwfr95+et5dTE53H38+BE+tE8e0Bg1f6kNBPFc1HrfsQyrq1X+elv+R0f+SOv0fUEsHCKhmSd+1BQAAxBoAAFBLAQIUABQACAAIAGSMwjyoZknftQUAAMQaAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAA7wUAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />
| |
| − |
| |
| − | | <ggb_applet width="396" height="402" version="3.2" ggbBase64="UEsDBBQACAAIAC+LwjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3V3rbttGFv69fQpCKIp2GzNzv6B2iyipXTduE8PZYrHdbkFJtMxYFlWKSuwUfaN9in2yPTND6kpRoi4xlSAAw+FwNPN955w558xwcvzd/V3PexcmwyjunzSwjxpe2G/HnajfPWmM0usj1fju28+Ou2HcDVtJ4F3HyV2QnjSoTxqmfBR9+9nfjoc38Xsv6Nkqv0Th+5PGddAbhg1vOEjCoDO8CcN0pjwY3Ue9KEgeXrXehu10OHngGjnvD0bwK2kygrL2XeciGua3T+0PDnpR+iJ6F3XCxOvF7ZOG4NB1+NcvYZJG7aB30mDIlZCTBpl7CEXUPL2Jk+hD3E9N9Unj11DiecPoQwhvIlN2/NQO9DgctXtRJwr6ZjC2H1DJ895HnfQGmtQCmgyj7k3qft221o7jpHP1MEzDO+/+X2ES2+74EiGJCVcaSSp4w3twjzDV8EjAaBTFlFMNGEKHoSdM+5ohgSWXEmuJmXlp+TP72+G7qzBNgcuhF9yHE5S7SdSZuTkfNuPepGgQR/30eTBIR4kVBJoVXaUP5ucAucSM8lm/2wuzMgI83YTt21Z8f2WRw9Q1/eZhYF+xHWp1n8e9OPESAwIMoJtdW+5q65iejmshWwfZGlkbptHxc6yJrWGvLXe1tXpR33UtGznOR41R/jPR0DMF0LiR3/Hge0ErBHloeKN+lF7kNyA3t9lQsXvh59FdCxRnWnLGbeJdtXn8dE7mjm/DpB/2nGT1gdtRPBp674wEu9+yHemE7egObt2DDJLA0PUP6IAr7YTdJMw77tTOAWafzkjvXPHx07wTpg9D6Gs7BfsB40nNWIx6p6BaJ407v+s3vE6QmlKjP73wLgTlSq1MWJEaY/OsMbYksTUKufpnzycow+NC+bCSFPQGNwGU+NkAesEDmIjpIdn2foo7swMN+gCYHQVo6sA0YCgZhGEnM4tpJsfeAJq0WjGFt4Vp6N2fNI6wz0ANhdCMYcww0wz01JUrKSiVQlNCCGXQ/gfXtm3CKZixJ7ZbNGPfIbYCu+angR3yFZrgpgjmDjqwlkJIKQXjgmtNlK4GXTu+uwv6Ha8f3EE3LsAyWLwiM8l4ATKy5wXYwOgwGqX5g65rKmtggQVjZMYgdxuzdie9AfXuh0PQZj6B4OkmTHFsqTKXily9ur4ehqkBV2oHpi5jckqOAXSCFBeYUCEIRZzY94lPFJEYI66IoDDXWCqITylBhDAMj7hQnM1b4RI0wj/6rs7Q2cLoDmb3dpRW0YDLT0UDxKykZxpAfSy0AI9AY4KQNlxspwDNaAggxcm6itCqoAit5YpAyhRhdq5czRjanK8pOS8Q6Icl4v/BmnEuucbAEVYCc8pkiaTPD3ddSZ/l67yfgk8AEM2R1XVktRbIel5O1qzmPF/UnHWIEMwyYS4td9kBF9jXGKScEMUUk4wi6sgQPuOaMkop14ghTS0X3JcU7sDyCM4IEpRvog0voh74J8V6gM1gvIBkkM6A/OyLYBAPv/kdVwF78tKjmqtpyLEvmdRgdQBABDbcIc4AW8yUoBCiICIq+iprIHy5GuHLTRC+XI5wVfuyI4i1DxYdIMYaMwouoAOYgCHhmAnCGYMoUG7l0hQi3FyNcHMThJt1k2EQYSQzcK1/nTkqTEokmcZIEcTYVlNmuZFYw0qQTawEqQvCYCWYz4TWglGisEL5LEmljyVCGCuNBBgQyfdnKNawFJVQvqwbylr7UjEIGAXThIDsZpYCcZ8KDTYEwWOpMNufqVjDVlTCuFk3jDGmEGSOA0yQWAsyZeB5cIEQxO4CohixDcSvkvQm7sb9oFcQal4uc9raFTzs9iF52EsCySLH2zjY0pcYiDCGnGKETRJg3w52KWGZlW8vENapQFjnkAgrjoiWBEQwLzCMsWaUY3AWhXhctprL2AorsBV+smxBhEWUJooq8JeQZvoj8LUsfG07qjoLVL2oMsO8qFH4ykxuQAiYPmBi4Vpyls/gPsza8JdKCGKBDr7D+HUFvOECvN9Xgff7+sCrfI441kjB/C0ZyHWWVxe+UAyBU8rgD+VM7RDcn6IkWUiSdZfZmMB5OxUsTf7GAdmbhcwYW5IYztxU6iOttWKUco4Y5/ufzpdpRMfxNsXSDHunVfTitD56AYQIzbhSHEvQD5OCz4Iz6mPElJIEIgrgbJdZs2UYh+UYn1XB+Kw+GGPiUyWIEJwwopHUeWymfA1xmUYamxQPZWyHGL+Oew/g5xT7o6cuTjuDCy1K2P8SQbPtW5zx8Tt29a9d/a69ZxCHrM79uE7kmI/b3YXJmloDmWYQczq93jVttnAVBpcvHg3Drrmb2OHfdzOgYoksGc/GEsmMI8eIUIQppoR0mXLswwQINlZReMaVduKofMo4kRLEkUkkd7ViYeWtZ1azxtYgivuLmxFuw3BgdoG86r9Jgv7QbCFydaY2OazJ0/WBsbQ4WapHmSwfgaruwanU0YJO8XzrxpxW0WzRmxGozLhJ7Suk1eGS1aonWZPdC9lCICXrUVkx51Rp+8KjU7n+0gRZY2WCVnHJJi/VJJ97RMzWCMwJ1loKgpXMdBbmPDq1DYuqnSfNT1djfLrJ+trpVutr+/B+CfE5VlhQs8UUE0UzbeRU+1SC3mAO8YUget/L8merIT/bBPKz+kGumI8pByNl1obHIR3jwpeAqsncmbgD7xvx5mrEm5sYkmbdDAnIONNEaI2FFBwwdnZE+EgBD5wTjSkG0B91FZltYqtZXSB+zFXk0zVQPt1khfN0qxXO/eQqkE844MgYk9p+QmBdHyEBUGxT0EbQd5kmLTPWpZCfbQL5Wf0gZ8TE2MZ1FBBCTBL/hEtfwwOEGVz2P0FWWcivZEyadTMmH2Mhf0vXegNjXRd0D8Kt3sBM18ZiHKBLvYGJrg/cB+dOb2Cc62I8PoYrvWRtJAPCrZCMb8hEIN1qyZLVqXxtY7qVYBwauvWT6Xa64xuzkrIeb8WrKVstA8+wPPNZSb8TuY9SoPqrrPb//vsivIbf6Px69VulVB2tIg8Vll5mYu8tR//xksUKrIRSnAowHVrahT+T15c+WBEMgm+XY5WbHsGaEx8CHooxIpQilENZy/TiihWY3YnqhKxiSb3y/u5deV/00m+8MVF7XwMwIaqZkQmTlDABJssSy7hvJgMC1HIiNSNuwYZRDm4oAT+JgxQogQ+X2O4+iN07XfNqmH9dMa+H2YoN0synwnxdB7O7ofhw+WptxddjrbHNqRdGPPfECvXriAlfMMSYguiZQrjBdrVf8SOszBRuHptxUbrLQseNA8h6eYJrh5FbfZxTiPNpOc6nm+J8ujXOe9kDRpT0tbF2oCFSYLfcyRhMTpTDJEa0yYns9LvJQtTPylE/2xT1s5qiLnzKkTTfnWGGpHROIISZPuPm22Blgh+2yxi+EPVmOerNTVFv1tGmLESXRcGl3MqglAaXBSFmQaBZEG6uFXQWhJ7TrV8vtt6dK5qEotsHpKtcDLS7sLQsKC07/oLwKoJUOSzdCwK7OdqjilvMl7jFMtv/UiVAnR9yzfzi64Mmbt4/Jqws/DxiRCCfwzyPNQIvipZuGKw5cd1DJm5e4VRxOohm+lYlDq05ba1Dpm3tcLQwGuX6cGib9exeb+TN5Uf2ZRyYS+WNnEdYZZtqSw+i2uVxbBBpYk0VFiY4Eiw/UQkJzcG+gmJSIbMtvRs6jFeZTsw6jK+dG3e54PIF5T7Zgiuyi4PFVjpg5+Xe+44+BceTbT4QBOnshDcC5YRpiYgxnVQz55cIn4MthQiWaGpOWyrbYF3lULGPkPtZcWZTsCATV1UCs6u11XdtrjfX7RK+fw5+tvza6wd3LVIvvmC77gcJ0Gr6nQ3pTXifQp/gwUnjiz9GcfpN9/I/f379l/u3fX8WsRReaMy+vR1o5Qtn6+sKL8MuGl4Eb8J/zopZdiTtMEyi67zT7nha0cjlO9sYP0yDJH1t0HVQXXhfe18efQlO4ldPPOTLrzZIL1wuSyxcVk8pXC5LJjzS4Uzm40klpVQwQ0jBtRD5h1QYa6k5o+DSSUlIxfmhWIDJggAfVRDg9fe7VQ+x1xdfVivxLZO1H1ZJ2RJPs3anQh7ZynaeRLs7NPZ89RlpBwcQ3iVAP34q8OwFnZefGjqVlWudpPEPbu48z/cP/eiSti8X5tIs8Upc/RtXO3K137q07u2qibYwlUt2vKuoyGmcPsM95xMX8EmX87l+wuFmjwPaecSTCxeaF656LmCXIx8dEvJoTq2PyCFD//aQoD/6pKT+9pBO58ml/igXe1Zv6Gfn0OdQmMRRZz6R5ma2X3944sFE+sT78Yn38rdxl/JaF1Xi0IsNvZdK2whKprsizrDK1YVs5qC14rgXBhMP4NwOEt4chQss7dFKTCc4JolfnJ2Zg4kohSUYWJ/Oln3+7/hdmBjJ/fNZ86/P1wuy6UyQPdXE68u/Pl8/2t7+y9R6pIGyLMf0WdOSIZbZZyaZMPuGNKfmeCM0c7bsNNZPp/+nF3Of/5dQ3/4fUEsHCM8TtlY4DQAARGoAAFBLAQIUABQACAAIAC+LwjzPE7ZWOA0AAERqAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAcg0AAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />
| |
| − | |}
| |
| | | | |
| | Die folgenden Lückentexte können Sie auch als Übungsblatt im pdf-Format herunterladen: | | Die folgenden Lückentexte können Sie auch als Übungsblatt im pdf-Format herunterladen: |
| Zeile 37: |
Zeile 32: |
| | | | |
| | Ebenenteilung: | | Ebenenteilung: |
| − | :Es seien <math>\ \epsilon</math> eine Ebene und <math>\ t</math> eine Gerade, die vollständig in <math>\ \epsilon</math> liegt. Ferner sei <math>\ Q</math> ein nicht zu <math>\ t</math> gehörender Punkt der Ebene <math>\ \epsilon</math>. Die Menge <math>\ \epsilon \setminus t</math> wird durch durch den Trenner <math>\ t</math> in genau zwei Klassen eingeteilt: | + | :Es seien <math>\ \varepsilon</math> eine Ebene und <math>\ t</math> eine Gerade, die vollständig in <math>\ \varepsilon</math> liegt. Ferner sei <math>\ Q</math> ein nicht zu <math>\ t</math> gehörender Punkt der Ebene <math>\ \varepsilon</math>. Die Menge <math>\ \varepsilon \setminus t</math> wird durch durch den Trenner <math>\ t</math> in genau zwei Klassen eingeteilt: |
| | | | |
| − | ::# Die Menge aller Punkte von <math>\ \epsilon \setminus t</math>, die mit <math>\ Q</math> auf derselben ... . | + | ::# Die Menge aller Punkte von <math>\ \varepsilon \setminus t</math>, die mit <math>\ Q</math> auf derselben ... . |
| − | ::# Die Menge aller Punkte von <math>\ \epsilon \setminus t</math>, die mit <math>\ Q</math> nicht auf derselben ... . | + | ::# Die Menge aller Punkte von <math>\ \varepsilon \setminus t</math>, die mit <math>\ Q</math> nicht auf derselben ... . |
| | | | |
| | === Definition des Begriffs der Halbebene === | | === Definition des Begriffs der Halbebene === |
| Zeile 46: |
Zeile 41: |
| | {| | | {| |
| | |- | | |- |
| − | | Zu unsere Vorstellung von der Eigenschaften einer beliebigen Ebene <math>\epsilon</math> gehört u.a., dass jede Gerade <math>\ g</math>, die zu unserer jeweiligen Ebene <math>\epsilon</math> gehört, diese in zwei ''Hälften'' bzw. zwei ''Seiten'' einteilt. Zur Kennzeichnung der beiden ''Seiten'' von <math>\epsilon</math> bezüglich der Geraden <math>\ g</math> verwenden wir einen Punkt <math>\ Q \in \epsilon</math>, welcher nicht zu <math>\ g</math> gehören sollte. | + | | Zu unsere Vorstellung von der Eigenschaften einer beliebigen Ebene <math>\varepsilon</math> gehört u.a., dass jede Gerade <math>\ g</math>, die zu unserer jeweiligen Ebene <math>\varepsilon</math> gehört, diese in zwei ''Hälften'' bzw. zwei ''Seiten'' einteilt. Zur Kennzeichnung der beiden ''Seiten'' von <math>\varepsilon</math> bezüglich der Geraden <math>\ g</math> verwenden wir einen Punkt <math>\ Q \in \varepsilon</math>, welcher nicht zu <math>\ g</math> gehören sollte. |
| | |[[Bild:Halbebene_00.png| 100 px]] | | |[[Bild:Halbebene_00.png| 100 px]] |
| | |- | | |- |
| − | | Zu der einen ''Hälfte'' von <math>\ \epsilon</math> bezüglich <math>\ g</math> gehören alle die Punkte aus <math>\epsilon \setminus g</math>, die mit <math>\ Q</math> auf derselben Seite von <math>\ g</math> liegen. Alle anderen Punkte aus <math>\epsilon \setminus g</math> gehören zur anderen Seite von <math>\ \epsilon</math> bezüglich <math>\ g</math>. | + | | Zu der einen ''Hälfte'' von <math>\ \varepsilon</math> bezüglich <math>\ g</math> gehören alle die Punkte aus <math>\varepsilon \setminus g</math>, die mit <math>\ Q</math> auf derselben Seite von <math>\ g</math> liegen. Alle anderen Punkte aus <math>\varepsilon \setminus g</math> gehören zur anderen Seite von <math>\ \varepsilon</math> bezüglich <math>\ g</math>. |
| | | [[Bild:Halbebene_01.png | 100 px]] | | | [[Bild:Halbebene_01.png | 100 px]] |
| | |} | | |} |
| | ==== Offene Halbebenen ==== | | ==== Offene Halbebenen ==== |
| − | Die beiden Seiten, in die die Menge der Punkte einer Ebene <math>\ \epsilon</math>, die nicht auf einer Geraden <math>\ g</math> dieser Ebene liegen, durch diese Gerade <math>\ g</math> eingeteilt wird, heißen offene Halbebenen von <math>\ \epsilon</math> bezüglich der Trägergeraden <math>\ g</math>. Der nicht zu <math>\ g</math> gehörende Referenzpunkt <math>\ Q \in \epsilon</math> bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich <math>\ g</math> mit <math>\ Q</math> auf derselben Seite liegen, wird mit <math>\ gQ^{+}</math> bezeichnet, die andere offene Halbebene von <math>\ \epsilon</math> bezüglich <math>\ g</math> und <math>\ Q</math> mit <math>\ gQ^{-}</math>. | + | Die beiden Seiten, in die die Menge der Punkte einer Ebene <math>\ \varepsilon</math>, die nicht auf einer Geraden <math>\ g</math> dieser Ebene liegen, durch diese Gerade <math>\ g</math> eingeteilt wird, heißen offene Halbebenen von <math>\ \varepsilon</math> bezüglich der Trägergeraden <math>\ g</math>. Der nicht zu <math>\ g</math> gehörende Referenzpunkt <math>\ Q \in \varepsilon</math> bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich <math>\ g</math> mit <math>\ Q</math> auf derselben Seite liegen, wird mit <math>\ gQ^{+}</math> bezeichnet, die andere offene Halbebene von <math>\ \varepsilon</math> bezüglich <math>\ g</math> und <math>\ Q</math> mit <math>\ gQ^{-}</math>. |
| | | | |
| − | Obige Ausführungen können als informelle Definition des Begriffs offene Halbebene dienen. Hinsichtlich wirklicher mathematischer Exaktheit der Festlegung, was denn eine offene Halbene sein möge, bedarf es einer genauereren Erklärung, was denn darunter zu verstehen wäre, dass zwei Punkte <math>\ P</math> und <math> \ Q</math> einer Ebene <math>\ \epsilon</math> auf ein und derselben bzw. auf zwei verschiedenen Seiten dieser Ebene bezüglich einer Geraden <math>\ g</math> liegen. | + | Obige Ausführungen können als informelle Definition des Begriffs offene Halbebene dienen. Hinsichtlich wirklicher mathematischer Exaktheit der Festlegung, was denn eine offene Halbene sein möge, bedarf es einer genauereren Erklärung, was denn darunter zu verstehen wäre, dass zwei Punkte <math>\ P</math> und <math> \ Q</math> einer Ebene <math>\ \varepsilon</math> auf ein und derselben bzw. auf zwei verschiedenen Seiten dieser Ebene bezüglich einer Geraden <math>\ g</math> liegen. |
| | | | |
| | ===== Definition IV.1: (offene Halbebene)===== | | ===== Definition IV.1: (offene Halbebene)===== |
| Zeile 68: |
Zeile 63: |
| | | | |
| | ===== Definition IV.2: (Halbebene) ===== | | ===== Definition IV.2: (Halbebene) ===== |
| − | ::Es sei <math>\ g</math> eine Gerade der Ebene <math>\ \epsilon</math>. <math>\ gQ^+</math> und <math>\ gQ^-</math> seien die beiden offenen Halbebenen von <math>\ \epsilon</math> bezüglich <math>\ g</math>. Unter den (geschlossenen) Halbebenen von <math>\ \epsilon</math> bezüglich <math>\ g</math> versteht die beiden Punktmengen, die durch die Vereinigung jeder dieser beiden offenen Halbebene von <math>\ \epsilon</math> bezüglich der Geraden <math>\ g</math> mit jeweils dieser Geraden <math>\ g</math> entstehen. | + | ::Es sei <math>\ g</math> eine Gerade der Ebene <math>\ \varepsilon</math>. <math>\ gQ^+</math> und <math>\ gQ^-</math> seien die beiden offenen Halbebenen von <math>\ \varepsilon</math> bezüglich <math>\ g</math>. Unter den (geschlossenen) Halbebenen von <math>\ \varepsilon</math> bezüglich <math>\ g</math> versteht die beiden Punktmengen, die durch die Vereinigung jeder dieser beiden offenen Halbebene von <math>\ \varepsilon</math> bezüglich der Geraden <math>\ g</math> mit jeweils dieser Geraden <math>\ g</math> entstehen. |
| | | | |
| | Bemerkung: Für die formale Beschreibung von offenen und geschlossenen Halbebenen wird jeweils dieselbe Bezsichnung verwendet: offene Halbebene: <math>\ g Q^+</math>, (geschlossene) Halbebene: <math>\ g Q^+</math>. Der weitere Gebrauch der Sprache kennzeichnet, ob es sich um eine offene oder um die geschlossene Halbene handeln soll. Aus Gründen der Vereinfachung sei vereinbart, dass <math>\ g Q^+</math> bzw. <math>\ g Q^-</math> immer die geschlossene Halbebene meint. Soll die offene Halbebene gemeint sein, so ist dieses durch den Zusatz "offen" zu kennzeichnen.<br /> | | Bemerkung: Für die formale Beschreibung von offenen und geschlossenen Halbebenen wird jeweils dieselbe Bezsichnung verwendet: offene Halbebene: <math>\ g Q^+</math>, (geschlossene) Halbebene: <math>\ g Q^+</math>. Der weitere Gebrauch der Sprache kennzeichnet, ob es sich um eine offene oder um die geschlossene Halbene handeln soll. Aus Gründen der Vereinfachung sei vereinbart, dass <math>\ g Q^+</math> bzw. <math>\ g Q^-</math> immer die geschlossene Halbebene meint. Soll die offene Halbebene gemeint sein, so ist dieses durch den Zusatz "offen" zu kennzeichnen.<br /> |
| Zeile 74: |
Zeile 69: |
| | ==== Definition IV.3: Halbraum==== | | ==== Definition IV.3: Halbraum==== |
| | | | |
| − | Gegeben sei eine Ebene E und ein Raum R, der E enthält. Die Punkte des Raumes, die nicht in E liegen, bilden zwei Mengen derart, dass gilt:<br /> | + | Gegeben sei eine Ebene <math>\varepsilon</math>.<br /> |
| − | :: Offener Halbraum <math>\ EQ^{+} :=\left\{ {P|\overline{PQ} \cap E=\phi } \right\}</math> | + | :: Halbraum <math>\varepsilon Q^{+} :=\left\{ P|... \right\} \cup \varepsilon</math> |
| − | :: Offener Halbraum <math>\ EQ^{-} :=\left\{ {P|\overline{PQ} \cap E=\left\{ {S} \right\} } \right\}</math><br /> | + | :: Halbraum <math>\varepsilon Q^{-} :=\left\{ P| ... \right\} \cup \varepsilon </math><br /> |
| − | Analog dazu komme ich zum Halbraum in dem ich den offenen Halbraum mit der Trennerebene vereinige.--[[Benutzer:RicRic|RicRic]] 22:40, 12. Dez. 2011 (CET)
| + | |
| | | | |
| | == Das Axiom von [http://de.wikipedia.org/wiki/Moritz_Pasch Pasch] == | | == Das Axiom von [http://de.wikipedia.org/wiki/Moritz_Pasch Pasch] == |
| Zeile 106: |
Zeile 100: |
| | | | |
| | | | |
| − | [[Category:Einführung_Geometrie]] | + | <!--- Was hier drunter steht muss stehen bleiben ---> |
| | + | |} |
| | + | </div> |
| | + | [[Kategorie:Einführung_S]] |
 eine Gerade und
eine Gerade und  ein Punkt auf ihr. Ferner sei
ein Punkt auf ihr. Ferner sei  ein von
ein von 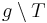 wird durch durch den Trenner
wird durch durch den Trenner  eine Ebene und
eine Ebene und 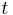 eine Gerade, die vollständig in
eine Gerade, die vollständig in 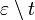 wird durch durch den Trenner
wird durch durch den Trenner  gehört u.a., dass jede Gerade
gehört u.a., dass jede Gerade 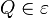 , welcher nicht zu
, welcher nicht zu 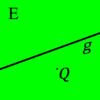
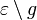 , die mit
, die mit 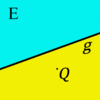
 bezeichnet, die andere offene Halbebene von
bezeichnet, die andere offene Halbebene von  .
.
 und
und 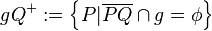
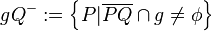
 und
und 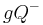 seien die beiden offenen Halbebenen von
seien die beiden offenen Halbebenen von 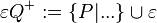
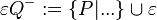
 . Ferner sei
. Ferner sei  geht. Wenn
geht. Wenn  von Punkten heißt konvex, wenn mit je zwei Punkten
von Punkten heißt konvex, wenn mit je zwei Punkten  und
und  dieser Menge die gesamte Strecke
dieser Menge die gesamte Strecke  zu
zu  und
und 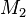 zwei konvexe Mengen.
zwei konvexe Mengen.

