Umkehrung von Implikationen SoSe 2018: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Beispiel 1 Teilbarkeit) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 8: | Zeile 8: | ||
Beide Implikationen, Ausgangsimplikation und zugehörige Umkehrung, müssen nicht zwangsläufig denselben Wahrheitsgehalt haben. | Beide Implikationen, Ausgangsimplikation und zugehörige Umkehrung, müssen nicht zwangsläufig denselben Wahrheitsgehalt haben. | ||
=Beispiele= | =Beispiele= | ||
| − | ==Beispiel 1 Teilbarkeit== | + | ==Beispiel 1: Teilbarkeit durch 3 und 9== |
===Implikation: Aus der Teilbarkeit durch 9 folgt die Teilbarkeit durch 3=== | ===Implikation: Aus der Teilbarkeit durch 9 folgt die Teilbarkeit durch 3=== | ||
Wenn eine Zahl <math>9</math> ein Teiler von <math>a</math> ist, dann ist <math>3</math> auch ein Teiler von <math>a</math>.<br /> | Wenn eine Zahl <math>9</math> ein Teiler von <math>a</math> ist, dann ist <math>3</math> auch ein Teiler von <math>a</math>.<br /> | ||
| Zeile 30: | Zeile 30: | ||
<math>\forall a \in \mathbb{Z}: 3 \mid a \Rightarrow 9 \mid a</math><br /> | <math>\forall a \in \mathbb{Z}: 3 \mid a \Rightarrow 9 \mid a</math><br /> | ||
Nun gibt es ganze Zahlen wie etwa <math>666</math> ([https://www.youtube.com/watch?v=WxnN05vOuSM the number of the biest]), die sowohl durch <math>3</math> als auch durch <math>9</math> teilbar sind. Weil aber z.B. <math>66</math> zwar durch <math>3</math>, aber nicht durch <math>9</math> teilbar ist, muss die Umkehrung unserer Ausgangsimplikation keine wahre Aussage. | Nun gibt es ganze Zahlen wie etwa <math>666</math> ([https://www.youtube.com/watch?v=WxnN05vOuSM the number of the biest]), die sowohl durch <math>3</math> als auch durch <math>9</math> teilbar sind. Weil aber z.B. <math>66</math> zwar durch <math>3</math>, aber nicht durch <math>9</math> teilbar ist, muss die Umkehrung unserer Ausgangsimplikation keine wahre Aussage. | ||
| + | ==Beispiel 2: In jedem Parallelogramm sind die gegenüberliegenden Seiten jeweils kongruent zueinander== | ||
| + | Der Begriff Parallelogramm sei entsprechend der Semantik der Begriffsbezeichnung definiert:<br /> | ||
| + | :Jedes Viereck mit zwei Paaren paralleler Seiten ist ein Parallelogramm. | ||
| + | ===Implikation=== | ||
| + | Wenn ein | ||
| + | ==Beispiel 3: Jauch reloaded== | ||
| + | === Implikation: Jedes Rechteck ist ein Parallelogramm=== | ||
| + | Unter einem Rechteck wollen wir ein Viereck verstehen, dessen Diagonalen kongruent zueinander sind und die sich gegenseitig halbieren.<br /> | ||
| + | Ein Parallelogramm sei als Viereck definiert, dessen gegenüberliegende Seiten jeweils kongruent zueinander sind.<br /> | ||
| + | Unsere Implikation spezifiziert sich wie folgt:<br /> | ||
| + | :Wenn sich in einem Viereck die Diagonalen halbierend und zueinander kongruent sind, dann sind die gegenüberliegenden Seiten dieses Vierecks jeweils kongruent zueinander. | ||
| + | Voraussetzung | ||
Version vom 29. April 2018, 10:22 Uhr
AllgemeinWir betrachten die Implikation BeispieleBeispiel 1: Teilbarkeit durch 3 und 9Implikation: Aus der Teilbarkeit durch 9 folgt die Teilbarkeit durch 3Wenn eine Zahl Unter der Voraussetzung, dass eine ganze Zahl Umkehrung: Aus der Teilbarkeit durch 3 folgt die Teilbarkeit durch 9Wenn eine Zahl durch Beispiel 2: In jedem Parallelogramm sind die gegenüberliegenden Seiten jeweils kongruent zueinanderDer Begriff Parallelogramm sei entsprechend der Semantik der Begriffsbezeichnung definiert:
ImplikationWenn ein Beispiel 3: Jauch reloadedImplikation: Jedes Rechteck ist ein ParallelogrammUnter einem Rechteck wollen wir ein Viereck verstehen, dessen Diagonalen kongruent zueinander sind und die sich gegenseitig halbieren.
Voraussetzung
|
 .
.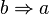 ist die Umkehrung der Implikation
ist die Umkehrung der Implikation 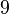 ein Teiler von
ein Teiler von  ist, dann ist
ist, dann ist  auch ein Teiler von
auch ein Teiler von 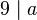
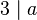
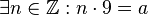 .
.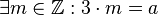 .
. existiert, die mit
existiert, die mit  gibt, die mit
gibt, die mit 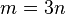 leistet das Verlangte:
leistet das Verlangte: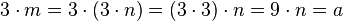 .
.
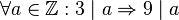
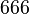 (
(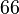 zwar durch
zwar durch 
