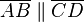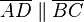Umkehrung von Implikationen SoSe 2018: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Implikation) |
*m.g.* (Diskussion | Beiträge) (→Beispiel 2: In jedem Parallelogramm sind die gegenüberliegenden Seiten jeweils kongruent zueinander) |
||
| Zeile 34: | Zeile 34: | ||
:Jedes Viereck mit zwei Paaren paralleler Seiten ist ein Parallelogramm. | :Jedes Viereck mit zwei Paaren paralleler Seiten ist ein Parallelogramm. | ||
===Implikation=== | ===Implikation=== | ||
| − | Wenn ein Viereck ein Parallelogramm ist, dann sind seine gegenüberliegenden Seiten jeweils kongruent zueinander. | + | :Wenn ein Viereck ein Parallelogramm ist, dann sind seine gegenüberliegenden Seiten jeweils kongruent zueinander.<br /> |
| + | Wir spezifizieren die Aussagen der Implikation bzgl. eines Vierecks <math>\overline{ABCD}</math>.<br /> | ||
| + | Voraussetzung: <math>\overline{ABCD}</math> ist ein Parallelogramm.<br /> | ||
| + | Behauptung: Die gegenüberliegenden Seiten von <math>\overline{ABCD</math> sind kongruent zueinander.<br /> | ||
| + | Wir formulieren Voraussetzung und Behauptung entsprechend der Eckpunktsbezeichnungen unseres Parallelogramms und wenden dabei die Definition des Begriffs Parallelogramm an:<br /> | ||
| + | Voraussetzung speziell formliert: <br /> | ||
| + | ::V<sub>1</sub>: <math>\overline{AB} \parallel \overline{CD}</math><br /> | ||
| + | ::V<sub>2</sub>: <math>\overline{AD} \parallel \overline{BC}</math><br /> | ||
==Beispiel 3: Jauch reloaded== | ==Beispiel 3: Jauch reloaded== | ||
Version vom 29. April 2018, 18:47 Uhr
AllgemeinWir betrachten die Implikation BeispieleBeispiel 1: Teilbarkeit durch 3 und 9Implikation: Aus der Teilbarkeit durch 9 folgt die Teilbarkeit durch 3Wenn eine Zahl Unter der Voraussetzung, dass eine ganze Zahl Umkehrung: Aus der Teilbarkeit durch 3 folgt die Teilbarkeit durch 9Wenn eine Zahl durch Beispiel 2: In jedem Parallelogramm sind die gegenüberliegenden Seiten jeweils kongruent zueinanderDer Begriff Parallelogramm sei entsprechend der Semantik der Begriffsbezeichnung definiert:
Implikation
Wir spezifizieren die Aussagen der Implikation bzgl. eines Vierecks sind kongruent zueinander. Wir formulieren Voraussetzung und Behauptung entsprechend der Eckpunktsbezeichnungen unseres Parallelogramms und wenden dabei die Definition des Begriffs Parallelogramm an:
Beispiel 3: Jauch reloadedImplikation: Jedes Rechteck ist ein ParallelogrammUnter einem Rechteck wollen wir ein Viereck verstehen, dessen Diagonalen kongruent zueinander sind und die sich gegenseitig halbieren.
Voraussetzung
|
 .
.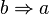 ist die Umkehrung der Implikation
ist die Umkehrung der Implikation 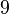 ein Teiler von
ein Teiler von  ist, dann ist
ist, dann ist  auch ein Teiler von
auch ein Teiler von 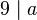
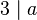
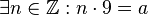 .
.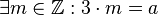 .
. existiert, die mit
existiert, die mit  gibt, die mit
gibt, die mit 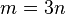 leistet das Verlangte:
leistet das Verlangte: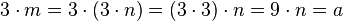 .
.
 (
( zwar durch
zwar durch  .
.