Übungsaufgaben zur Algebra, Serie 4 SoSe 2018: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 4.2) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 4.2) |
||
| Zeile 12: | Zeile 12: | ||
dass <br /> | dass <br /> | ||
<math>\begin{matrix} \lambda a_1 &=& a_2 \\ \lambda b_1 &=& b_2 \\ \lambda c_1 &=& c_2 \end{matrix}</math> <br /> | <math>\begin{matrix} \lambda a_1 &=& a_2 \\ \lambda b_1 &=& b_2 \\ \lambda c_1 &=& c_2 \end{matrix}</math> <br /> | ||
| − | gilt. | + | gilt.<br /> |
| + | (a) Beweisen Sie: Die Relation Gleichung b ist Linearkombination von Gleichung a ist eine Äquivalenzrelation auf der Mange der Gleichungen vom Typ <math>ax +by=c</math>.<br /> | ||
| + | (b) Interpretieren Sie die Relation geometrisch. | ||
=Aufgabe 4.3= | =Aufgabe 4.3= | ||
Version vom 12. Mai 2018, 14:28 Uhr
Aufgabe 4.1Wir betrachten auf der Menge der natürlichen Zahlen, die Relationen Teiler und echter Teiler. Aufgabe 4.2Die Gleichung Aufgabe 4.3Aufgabe 4.4Aufgabe 4.5Aufgabe 4.6Aufgabe 4.7Aufgabe 4.8Aufgabe 4.9Aufgabe 4.10 |
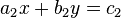 ist eine Linearkombination der Gleichung
ist eine Linearkombination der Gleichung 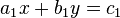 , wenn eine Zahl
, wenn eine Zahl 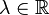 derart existiert,
dass
derart existiert,
dass 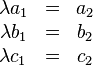
 .
.
