Übungsaufgaben zur Algebra, Serie 4 SoSe 2018: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 4.2)
(→‎Aufgabe 4.3)
Zeile 17: Zeile 17:
  
 
=Aufgabe 4.3=
 
=Aufgabe 4.3=
−
 
+
Es sei <math>G_2</math> die Menge aller Gleichungen vom Typ <math>ax+by=c</math>. <math>\mathbb{G}</math> sei die Menge aller Äquivalenzklassen <math>\overline{g}</math>, in die <math>G</math> durch die Äquivalenzrelation ''Gleichung a ist Linearkombination von Gleichung b'' eingeteilt wird. Wir definieren auf <math>\mathbb{G}</math> die folgende Operation <math>\oplus</math>: <math>\forall \overline{a}, \overline{b} \in \mathbb{G}: \overline{a} \oplus \overline{b} := \overline{a+b}</math>. Beweisen Sie: <math>[\mathbb{G}, \oplus]</math> ist Gruppe.
  
 
=Aufgabe 4.4=
 
=Aufgabe 4.4=

Version vom 13. Mai 2018, 10:38 Uhr

Inhaltsverzeichnis

Aufgabe 4.1

Wir betrachten auf der Menge der natürlichen Zahlen, die Relationen Teiler und echter Teiler.
(a) Eine dieser Relationen ist keine Äquivalenzrelationen. Welche? Beweisen Sie Ihre Aussage.
(b) Beweisen Sie für die andere Relation, dass sie eine Äquivalanzrelation ist.

Aufgabe 4.2

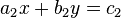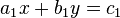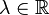Die Gleichung a_2x+b_2y=c_2 ist eine Linearkombination der Gleichung a_1x+b_1y=c_1, wenn eine Zahl \lambda \in \mathbb{R} derart existiert, dass
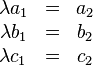
\begin{matrix} \lambda a_1 &=& a_2 \\ \lambda b_1 &=& b_2 \\ \lambda c_1 &=& c_2 \end{matrix}
gilt.
(a) Beweisen Sie: Die Relation Gleichung b ist Linearkombination von Gleichung a ist eine Äquivalenzrelation auf der Menge der Gleichungen vom Typ ax +by=c.
(b) Interpretieren Sie die Relation geometrisch.

Aufgabe 4.3

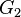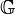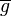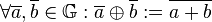Es sei G_2 die Menge aller Gleichungen vom Typ ax+by=c. \mathbb{G} sei die Menge aller Äquivalenzklassen \overline{g}, in die G durch die Äquivalenzrelation Gleichung a ist Linearkombination von Gleichung b eingeteilt wird. Wir definieren auf \mathbb{G} die folgende Operation \oplus: \forall \overline{a}, \overline{b} \in \mathbb{G}: \overline{a} \oplus \overline{b} := \overline{a+b}. Beweisen Sie: [\mathbb{G}, \oplus] ist Gruppe.

Aufgabe 4.4

Aufgabe 4.5

Aufgabe 4.6

Aufgabe 4.7

Aufgabe 4.8

Aufgabe 4.9

Aufgabe 4.10

Von „http://geometrie.zum.de/index.php?title=Übungsaufgaben_zur_Algebra,_Serie_4_SoSe_2018&oldid=31487“