Lösung von Aufgabe 2.7 SoSe 2018: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=90%| style="backgro…“) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 4: | Zeile 4: | ||
<!--- Was hier drüber steht muss stehen bleiben ---> | <!--- Was hier drüber steht muss stehen bleiben ---> | ||
| + | =Aufgabe 2.6 SoSe 2018= | ||
| + | Wir setzen den Innenwinkelsatz für Dreiecke und den Nebenwinkelsatz als bewiesen voraus.<br /> | ||
| + | '''Satz: (starker Außenwinkelsatz)''' | ||
| + | :Jeder Außenwinkel eines Dreiecks ist so groß wie die Summe der Größen der beiden nicht anliegenden Innenwinkel. <br /> | ||
| + | a) Formulieren Sie den starken Außenwinkelatz in ''Wenn-Dann-Form''.<br /> | ||
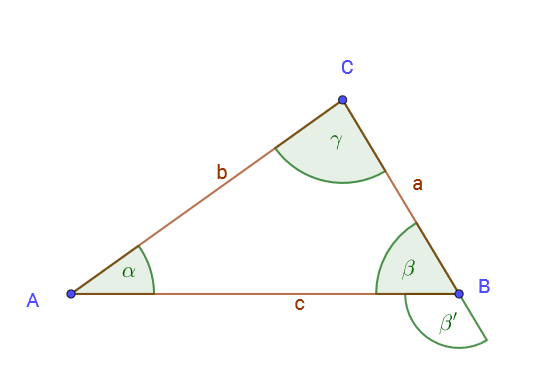
| + | b) Formulieren Sie die Voraussetzung und die Behauptung des starken Außenwinkelsatzes unter Verwendung der Bezeichnungen in der folgenden Skizze:<br /> | ||
| − | + | [[Datei:Außenwinkelsatz.png|Skizze für den Beweis des starken Außenwinkelsatzes]]<br /> | |
| + | c) Beweisen Sie den starken Außenwinkelsatz.<br /> | ||
| + | =Lösung= | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
Version vom 22. Mai 2018, 11:27 Uhr
Aufgabe 2.6 SoSe 2018Wir setzen den Innenwinkelsatz für Dreiecke und den Nebenwinkelsatz als bewiesen voraus.
a) Formulieren Sie den starken Außenwinkelatz in Wenn-Dann-Form.
Lösung |
