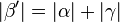Lösung von Aufgabe 2.7 SoSe 2018: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Lösung)
(→‎Teilaufgabe b))
 
(3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 15: Zeile 15:
 
=Lösung=
 
=Lösung=
 
==Teilaufgabe a)==
 
==Teilaufgabe a)==
−
Wenn ein Winkel <math> \beta '</math> ein Außenwinkel eines Dreiecks <math> \overline{ABC} </math> ist, dann ist seine Größe gleich der Summe der Größen der beiden Innenwinkel von <math> \overline{ABC}</math>, die keine Nebenwinkel zu <math> \beta '</math> sind.
+
Wenn ein Winkel <math> ~\beta '</math> ein Außenwinkel eines Dreiecks <math> \overline{ABC} </math> ist, dann ist seine Größe gleich der Summe der Größen der beiden Innenwinkel von <math> \overline{ABC}</math>, die keine Nebenwinkel zu <math> ~\beta '</math> sind.
  
 
==Teilaufgabe b)==
 
==Teilaufgabe b)==
 
===Voraussetzung===
 
===Voraussetzung===
−
<math> \beta'</math> ist Außenwinkel von <math> \overline{ABC} </math>.
+
<math> ~\beta'</math> ist Außenwinkel von <math> \overline{ABC} </math>.
 +
===Behauptung===
 +
<math>\vert \beta' \vert = \vert \alpha \vert + \vert \gamma \vert</math>
  
 
==Teilaufgabe c)==
 
==Teilaufgabe c)==

Aktuelle Version vom 22. Mai 2018, 11:48 Uhr

Inhaltsverzeichnis

Aufgabe 2.6 SoSe 2018

Wir setzen den Innenwinkelsatz für Dreiecke und den Nebenwinkelsatz als bewiesen voraus.
Satz: (starker Außenwinkelsatz)

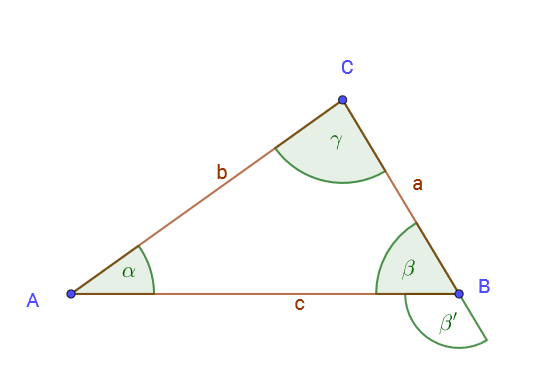
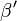Jeder Außenwinkel eines Dreiecks ist so groß wie die Summe der Größen der beiden nicht anliegenden Innenwinkel.

a) Formulieren Sie den starken Außenwinkelatz in Wenn-Dann-Form.
b) Formulieren Sie die Voraussetzung und die Behauptung des starken Außenwinkelsatzes unter Verwendung der Bezeichnungen in der folgenden Skizze:

Skizze für den Beweis des starken Außenwinkelsatzes
c) Beweisen Sie den starken Außenwinkelsatz.

Lösung

Teilaufgabe a)

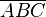Wenn ein Winkel ~\beta ' ein Außenwinkel eines Dreiecks \overline{ABC} ist, dann ist seine Größe gleich der Summe der Größen der beiden Innenwinkel von \overline{ABC}, die keine Nebenwinkel zu ~\beta ' sind.

Teilaufgabe b)

Voraussetzung

~\beta' ist Außenwinkel von \overline{ABC} .

Behauptung

\vert \beta' \vert = \vert \alpha \vert + \vert \gamma \vert

Teilaufgabe c)

\begin{matrix} \text{Nr.} & \text{Beweisschritt} & \text{Begründung des Beweisschrittes} \\ (1) & \beta' \text{ und } \beta \text{ sind Nebenwinkel.} & \text{Voraussetzung, Definition Außenwinkel} \\ (2) & \vert \beta \vert + \vert \beta' \vert = 180^\circ & \text{ (1), Nebenwinkelsatz} \\ (3) & \vert \alpha \vert + \vert \beta \vert + \vert \gamma \vert = 180^\circ & \text{Innenwinkelsatz für Dreiecke} \\ (4) & \vert \alpha \vert + \vert \beta \vert + \vert \gamma \vert = \vert \beta \vert + \vert \beta' \vert & \text{(2), (3)} \\ (5) & \vert \alpha \vert + \vert \gamma \vert = \vert \beta' \vert & \text{(4), q.e.d.} \\ \end{matrix}

Behauptung

\vert \beta' \vert = \vert \alpha \vert + \vert \gamma \vert

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_2.7_SoSe_2018&oldid=31642“