Lemmata zu Winkeln: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Lemma W/3) |
||
| Zeile 17: | Zeile 17: | ||
::Liegt ein Punkt <math>P</math> im Inneren eines Winkels mit dem Scheitel <math>S</math>, dann liegt der gesamte Strahl <math>SP^+</math> im Inneren dieses Winkels. | ::Liegt ein Punkt <math>P</math> im Inneren eines Winkels mit dem Scheitel <math>S</math>, dann liegt der gesamte Strahl <math>SP^+</math> im Inneren dieses Winkels. | ||
===Lemma W/3=== | ===Lemma W/3=== | ||
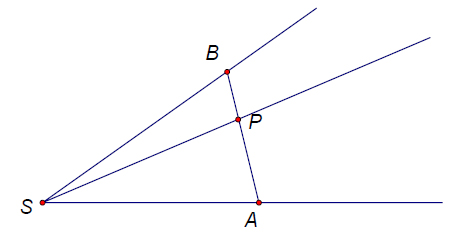
| − | ::Es seien <math>A,B,S</math> drei nichtkollineare Punkte. | + | ::Es seien <math>A,B,S</math> drei nichtkollineare Punkte. Wenn der Punkt <math>P</math> im Inneren des Winkels <math>\angle ASB</math> und nicht auf den Schenkeln dieses Winkels liegt, dann schneidet der Strahl <math>SP^+</math> die offene Strecke <math>\overline{AB}</math>. |
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
Aktuelle Version vom 10. Juni 2018, 12:34 Uhr
VorbemerkungenUnter einem Lemma versteht der Mathematiker einen Hilfssatz. Wir geben hier die folgenden Hilfssätze an, die wir im weiteren verwenden werden, ohne sie hier bewiesen zu haben. Die Beweise dieser Lemmata sind nicht wirklich schwer aber unerquicklich. Wer sich für die Beweise interessiert findet sie hier: Lemma W/1
Lemma W/2
Lemma W/3
|
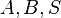. Wenn 
ein Punkt der offenen Strecke 
ist, dann liegt der Strahl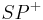 
vollständig im Inneren von 
.
, dann liegt der gesamte Strahl 
