Der Innenwinkelsatz für Dreiecke: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Satz XII.4: (Innenwinkelsatz für Dreiecke)) |
*m.g.* (Diskussion | Beiträge) (→Beweis von Satz XII.4) |
||
| Zeile 7: | Zeile 7: | ||
===== Satz XII.4: (Innenwinkelsatz für Dreiecke)===== | ===== Satz XII.4: (Innenwinkelsatz für Dreiecke)===== | ||
:: Es sei <math>\overline{ABC}</math> ein Dreieck mit den Innenwinkeln <math>\alpha = \angle CBA</math>, <math>\beta = \angle CBA</math> und <math>\gamma = \angle ACB</math>. <br />Es gilt <math>\left| \alpha \right| + \left| \beta \right| + \left| \gamma \right| = 180</math>. | :: Es sei <math>\overline{ABC}</math> ein Dreieck mit den Innenwinkeln <math>\alpha = \angle CBA</math>, <math>\beta = \angle CBA</math> und <math>\gamma = \angle ACB</math>. <br />Es gilt <math>\left| \alpha \right| + \left| \beta \right| + \left| \gamma \right| = 180</math>. | ||
| − | + | ||
| − | + | ||
===== Beweis von Satz XII.4 (Innenwinkelsatz für Dreiecke) ===== | ===== Beweis von Satz XII.4 (Innenwinkelsatz für Dreiecke) ===== | ||
===== Satz XII.5: (Starker Außenwinkelsatz) ===== | ===== Satz XII.5: (Starker Außenwinkelsatz) ===== | ||
Version vom 15. Juli 2010, 10:06 Uhr
Inhaltsverzeichnis[Verbergen] |
"Der Abreißbeweis"
Diskutieren Sie Sinn und Unsinn des folgenden "Beweises":
http://www.ph-heidelberg.de/wp/gieding/Lehre/didaktik_5_8/flash/innenwinkelsumme.swf
Ein echter Beweis
Satz XII.4: (Innenwinkelsatz für Dreiecke)
- Es sei
ein Dreieck mit den Innenwinkeln 
, 
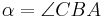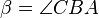und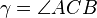 
.
Es gilt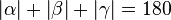
.
- Es sei
