Lösung von Aufgabe 5.3 P (SoSe 18): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| (5 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
| − | a) Menge Drachen: {Q,Re,Ra,D} <br /> | + | a) Menge Drachen: M={Q,Re,Ra,D} <br /> |
| − | b) | + | b) Kreuzprodukt: {(Q,Q),(Q,Re),(Q,Ra),(Q,D),(Re,Ra),....,(D,D)} <br /> |
| + | c) Relation R: R= {(Q,Q),(Re,Re),(Re,Ra),(Ra,Re),(Ra,Ra),(D,D)} <br /> | ||
| + | d) Die Relation ist reflexiv. <br /> | ||
| + | |||
| + | zu c) da fehlt noch was? | ||
| + | zu d) wie sieht es mit Symmetrie und Transitivität aus? --[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 09:58, 28. Mai 2018 (CEST) | ||
| + | |||
| + | zu d) Die Relation ist reflexiv und transitiv oder? | ||
| + | jetzt stimmt es bei d), aber bei c) fehlt immer noch was.--[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 12:02, 18. Jun. 2018 (CEST) | ||
Aktuelle Version vom 18. Juni 2018, 12:02 Uhr
a) Geben Sie die Menge 
aller konvexer Drachenvierecke an.
b) Bilden Sie das kartesische Produkt der Menge 
.
c) Wir definineren eine Relation 
mit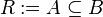 
. Bestimmen Sie die Relation auf .
d) Untersuchen Sie die Relation auf ihre Eigenschaften (reflexiv, symmetrisch, transitiv).
a) Menge Drachen: M={Q,Re,Ra,D}
b) Kreuzprodukt: {(Q,Q),(Q,Re),(Q,Ra),(Q,D),(Re,Ra),....,(D,D)}
c) Relation R: R= {(Q,Q),(Re,Re),(Re,Ra),(Ra,Re),(Ra,Ra),(D,D)}
d) Die Relation ist reflexiv.
zu c) da fehlt noch was? zu d) wie sieht es mit Symmetrie und Transitivität aus? --Schnirch (Diskussion) 09:58, 28. Mai 2018 (CEST)
zu d) Die Relation ist reflexiv und transitiv oder?
jetzt stimmt es bei d), aber bei c) fehlt immer noch was.--Schnirch (Diskussion) 12:02, 18. Jun. 2018 (CEST)
