Lösung von Aufgabe 8.4: Unterschied zwischen den Versionen
| (4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Definieren Sie den Begriff des Dreiecks, den Begriff des Innenwinkel eines Dreiecks und den Begriff des Inneren eines Dreiecks. | Definieren Sie den Begriff des Dreiecks, den Begriff des Innenwinkel eines Dreiecks und den Begriff des Inneren eines Dreiecks. | ||
| + | ==Lösung --[[Benutzer:Schnirch|Schnirch]] 10:09, 15. Jul. 2010 (UTC)== | ||
| + | '''Definition (Dreieck):''' <br\> | ||
| + | Es seien <math>\ A</math>, <math>\ B </math> und <math>\ C </math> drei nicht kollineare Punkte. Die Vereinigungsmenge der Strecken <math> \overline { AB } </math>, <math> \overline { BC } </math> und <math> \overline { AC } </math> heißt Dreieck <math> \overline { ABC } </math>. <br /> | ||
| + | |||
| + | '''Definition (Innenwinkel eines Dreiecks):''' <br\> | ||
| + | Gegeben sei ein Dreieck <math> \overline { ABC } </math>. Die Winkel <math> \angle {AB^{+}AC^{+}} </math> <math> \angle {BC^{+}BA^{+}} </math> und <math> \angle {CB^{+}CA^{+}} </math> heißen Innenwinkel des Dreiecks <math> \overline { ABC } </math>. <br\> | ||
| + | |||
| + | '''Definition (Inneres eines Dreiecks):''' <br\> | ||
| + | Das Innere eines Dreiecks <math> \overline { ABC } </math> ist die Schnittmenge der drei Halbebenen <math>\ ABC^{+} </math>, <math>\ BCA^{+} </math> und <math>\ ACB^{+} </math>. Kurzschreibweise: <math>\ I( \overline { ABC }):=\ ABC^{+}\cap BCA^{+}\cap ACB^{+}</math> | ||
| + | |||
| + | ==vorangegangene Diskussion== | ||
Es seien <math> A</math>, <math> B </math> und <math> C </math> drei nicht kollineare Punkte. Die Vereinigungsmenge der Strecken <math> \overline { AB } </math>, <math> \overline { BC } </math> und <math> \overline { AC } </math> heißt Dreieck <math> \overline { ABC } </math>. <br /> <math> \overline { AB } </math>, <math> \overline { BC } </math> und <math> \overline { AC } </math> heißen Seiten des Dreiecks <math> \overline { ABC } </math>. Die Winkel zwischen zwei benachbarten Seiten des Dreiecks <math> \overline { ABC } </math> heißen Innenwinkel. <br/> Inneres des Dreiecks <math> \overline { ABC } </math> heißt eine Punktmenge der Ebene <math> E </math>, in der der Punkte <math> A</math>, <math> B </math> und <math> C </math> liegen, die von <math> \overline { AB } </math>, <math> \overline { BC } </math> und <math> \overline { AC } </math> umschlossen wird. <br /> --[[Benutzer:Maude001|Maude001]] 17:55, 19. Jun. 2010 (UTC) | Es seien <math> A</math>, <math> B </math> und <math> C </math> drei nicht kollineare Punkte. Die Vereinigungsmenge der Strecken <math> \overline { AB } </math>, <math> \overline { BC } </math> und <math> \overline { AC } </math> heißt Dreieck <math> \overline { ABC } </math>. <br /> <math> \overline { AB } </math>, <math> \overline { BC } </math> und <math> \overline { AC } </math> heißen Seiten des Dreiecks <math> \overline { ABC } </math>. Die Winkel zwischen zwei benachbarten Seiten des Dreiecks <math> \overline { ABC } </math> heißen Innenwinkel. <br/> Inneres des Dreiecks <math> \overline { ABC } </math> heißt eine Punktmenge der Ebene <math> E </math>, in der der Punkte <math> A</math>, <math> B </math> und <math> C </math> liegen, die von <math> \overline { AB } </math>, <math> \overline { BC } </math> und <math> \overline { AC } </math> umschlossen wird. <br /> --[[Benutzer:Maude001|Maude001]] 17:55, 19. Jun. 2010 (UTC) | ||
| + | |||
| + | Bemerkung: Das Innere eines Dreiecks ist die Menge der Punkte, die von den Dreiecksseiten umschlossen wird. Das wäre die intuitive Vorstellung, mit der wir in der Schule arbeiten können. Was bedeutet aber ''umschließen'' ? Sie bleiben bei der richtigen intuitiven Vorstellung, hier müssen Sie jedoch präziser werden. Entwickeln Sie eine Definition des Begriffs ''die Seiten eines Dreiecks umschließen eine Menge von Punkten.''--[[Benutzer:*m.g.*|*m.g.*]] 13:15, 22. Jun. 2010 (UTC) | ||
Alternativ für das Innere des Dreiecks: | Alternativ für das Innere des Dreiecks: | ||
Es sei <math>a</math> die Gerade durch die Punkte <math> C</math> und <math>B</math>, <math>b</math> die Gerade durch die Punkte <math>A</math> und <math>C</math>, <math>c</math> die Gerade durch die Punkte <math>A</math> und <math>B</math>. | Es sei <math>a</math> die Gerade durch die Punkte <math> C</math> und <math>B</math>, <math>b</math> die Gerade durch die Punkte <math>A</math> und <math>C</math>, <math>c</math> die Gerade durch die Punkte <math>A</math> und <math>B</math>. | ||
| − | Das Innere eines Dreiecks ist der Durchschnitt der drei Halbebenen <math>aA</math>+, <math>bB</math>+ und <math>cC</math>+. | + | Das Innere eines Dreiecks ist der Durchschnitt der drei Halbebenen <math>aA</math>+, <math>bB</math>+ und <math>cC</math>+. |
| + | --[[Benutzer:*Bambi*|*Bambi*]] 07:52, 22. Jun. 2010 (UTC) | ||
| + | |||
| + | Bemerkung: Diese Definition ist absolut korrekt. Deshalb ist sie keine Alternative zu der Definition von user Maude001 sondern eine Weiterentwicklung bzw. Präzisierung dessen, was Umschließen in diesem Kontext bedeutet.--[[Benutzer:*m.g.*|*m.g.*]] 13:15, 22. Jun. 2010 (UTC) | ||
Aktuelle Version vom 15. Juli 2010, 11:09 Uhr
Definieren Sie den Begriff des Dreiecks, den Begriff des Innenwinkel eines Dreiecks und den Begriff des Inneren eines Dreiecks.
Lösung --Schnirch 10:09, 15. Jul. 2010 (UTC)
Definition (Dreieck):
Es seien  ,
,  und
und  drei nicht kollineare Punkte. Die Vereinigungsmenge der Strecken
drei nicht kollineare Punkte. Die Vereinigungsmenge der Strecken  ,
,  und
und  heißt Dreieck
heißt Dreieck  .
.
Definition (Innenwinkel eines Dreiecks):
Gegeben sei ein Dreieck  . Die Winkel
. Die Winkel 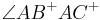
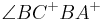 und
und 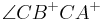 heißen Innenwinkel des Dreiecks
heißen Innenwinkel des Dreiecks  .
.
Definition (Inneres eines Dreiecks):
Das Innere eines Dreiecks  ist die Schnittmenge der drei Halbebenen
ist die Schnittmenge der drei Halbebenen 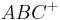 ,
, 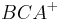 und
und 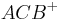 . Kurzschreibweise:
. Kurzschreibweise: 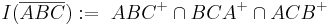
vorangegangene Diskussion
Es seien  ,
,  und
und  drei nicht kollineare Punkte. Die Vereinigungsmenge der Strecken
drei nicht kollineare Punkte. Die Vereinigungsmenge der Strecken  ,
,  und
und  heißt Dreieck
heißt Dreieck  .
.
 ,
,  und
und  heißen Seiten des Dreiecks
heißen Seiten des Dreiecks  . Die Winkel zwischen zwei benachbarten Seiten des Dreiecks
. Die Winkel zwischen zwei benachbarten Seiten des Dreiecks  heißen Innenwinkel.
heißen Innenwinkel.
Inneres des Dreiecks  heißt eine Punktmenge der Ebene
heißt eine Punktmenge der Ebene  , in der der Punkte
, in der der Punkte  ,
,  und
und  liegen, die von
liegen, die von  ,
,  und
und  umschlossen wird.
umschlossen wird.
--Maude001 17:55, 19. Jun. 2010 (UTC)
Bemerkung: Das Innere eines Dreiecks ist die Menge der Punkte, die von den Dreiecksseiten umschlossen wird. Das wäre die intuitive Vorstellung, mit der wir in der Schule arbeiten können. Was bedeutet aber umschließen ? Sie bleiben bei der richtigen intuitiven Vorstellung, hier müssen Sie jedoch präziser werden. Entwickeln Sie eine Definition des Begriffs die Seiten eines Dreiecks umschließen eine Menge von Punkten.--*m.g.* 13:15, 22. Jun. 2010 (UTC)
Alternativ für das Innere des Dreiecks:
Es sei  die Gerade durch die Punkte
die Gerade durch die Punkte  und
und  ,
,  die Gerade durch die Punkte
die Gerade durch die Punkte  und
und  ,
,  die Gerade durch die Punkte
die Gerade durch die Punkte  und
und  .
Das Innere eines Dreiecks ist der Durchschnitt der drei Halbebenen
.
Das Innere eines Dreiecks ist der Durchschnitt der drei Halbebenen 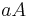 +,
+, 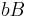 + und
+ und 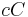 +.
--*Bambi* 07:52, 22. Jun. 2010 (UTC)
+.
--*Bambi* 07:52, 22. Jun. 2010 (UTC)
Bemerkung: Diese Definition ist absolut korrekt. Deshalb ist sie keine Alternative zu der Definition von user Maude001 sondern eine Weiterentwicklung bzw. Präzisierung dessen, was Umschließen in diesem Kontext bedeutet.--*m.g.* 13:15, 22. Jun. 2010 (UTC)

