Lösung von Aufgabe 7.9: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: Definieren Sie mittels des Schnitts geeigneter Halbebenen den Begriff des Inneren eines Dreiecks <math>\overline{ABC}</math>.) |
|||
| (7 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Definieren Sie mittels des Schnitts geeigneter Halbebenen den Begriff des Inneren eines Dreiecks <math>\overline{ABC}</math>. | Definieren Sie mittels des Schnitts geeigneter Halbebenen den Begriff des Inneren eines Dreiecks <math>\overline{ABC}</math>. | ||
| + | |||
| + | ==Lösung--[[Benutzer:Schnirch|Schnirch]] 10:12, 15. Jul. 2010 (UTC)== | ||
| + | |||
| + | '''Definition (Inneres eines Dreiecks):''' <br\> | ||
| + | Das Innere eines Dreiecks <math> \overline { ABC } </math> ist die Schnittmenge der drei Halbebenen <math>\ ABC^{+} </math>, <math>\ BCA^{+} </math> und <math>\ ACB^{+} </math>. Kurzschreibweise: <math>\ I( \overline { ABC }):=\ ABC^{+}\cap BCA^{+}\cap ACB^{+}</math> | ||
| + | |||
| + | ==vorangegangene Diskussion== | ||
| + | |||
| + | 1)<math>\overline{AB}</math> = g | ||
| + | |||
| + | gC <math> \ OA^+ \ </math> := {P| Punkt, der links von g liegt} | ||
| + | |||
| + | --[[Benutzer:Nicola|Nicola]] 13:48, 6. Jun. 2010 (UTC) | ||
| + | |||
| + | |||
| + | 2):<math>\overline{ABC}</math> sei ein Dreieck und <math>\ a,b,c</math> drei Geraden mit <math>\overline{BC} \subset a, \ \ \overline{AC} \subset b, \ \ \overline{AB} \subset c</math>. Die Punktmenge <math>I = aA^+ \cap bB^+ \cap cC^+ \setminus \overline{ABC}</math> heißt das Innere des Dreiecks <math>\overline{ABC}</math>. | ||
| + | :--[[Benutzer:Sternchen|Sternchen]] 17:20, 10. Jun. 2010 (UTC) | ||
| + | |||
| + | Kommentar --[[Benutzer:*m.g.*|*m.g.*]] 22:03, 29. Jun. 2010 (UTC) | ||
| + | |||
| + | Die Definition ist völlig korrekt. Ob man die Dreiecksseiten selbst mit zum Inneren des Dreiecks rechnet oder besser nicht, ist Ansichtssache. Sie möchten sie nicht zum Inneren rechnen. Das bleibt Ihnen unbenommen. Weil ich wegen diverser zukünftiger Beweisführungen gerne hätte, dass zum Inneren eines Winkels auch seine Schenkel gehören, würde ich persönlich bevorzugen, wenn die Dreicksseiten auch zum Inneren des Dreiecks gehören. Das braucht Sie aber nicht zu stören. Sie werden bei meinen zukünftigen Beweisen (etwa das was sich im Dunstkreis des schwachen Außenwinkelsatzes abspielen wird) sicherlich erkennen, dass ich nur aus Gründen von Formulierungsfaulheiten die Schenkel eines Winkels gern zu seinem Inneren (und damit auch die Dreiecksseiten zum Inneren eines Dreiecks) rechnen möchte. | ||
| + | |||
| + | 3)Gegeben seien drei nicht kollineare Punkte A, B und C. Die Schnittmenge der offenen Halbebenen ACB<sup>+</sup>, BCA<sup>+</sup> und ABC<sup>+</sup> heißt das Innere des Dreiecks <math>\overline{ABC}</math>. | ||
| + | |||
| + | Kommentar --[[Benutzer:*m.g.*|*m.g.*]] 22:17, 29. Jun. 2010 (UTC) | ||
| + | Das ist genau so korrekt wie 2). Es wurde nur effizienter formuliert (Ob das in der momentanen Situation für die Allgemeinheit auch didaktisch effizienter ist sei dahingestellt.). Weil eine Gerade durch zwei verschiedene Punkte eindeutig bestimmt ist, kann man sie durch diese beiden Punkte auch eindeutig beschreiben. Ich glaube, dass Ihre Schreibweise für die Studierenden leichter zu verstehen ist, wenn man die Gerade <math>\ AB</math> durch ein Komma von dem Referenzpunkt<math> \ C</math> der Halbene trennt: <math>\ AB,C^+</math>. Ob dem wirklich so ist weiß ich nicht, ich kann es mir nur vorstellen. Aber vorstellen kann man sich viel. Rückkopplung? | ||
Aktuelle Version vom 15. Juli 2010, 12:12 Uhr
Definieren Sie mittels des Schnitts geeigneter Halbebenen den Begriff des Inneren eines Dreiecks  .
.
Lösung--Schnirch 10:12, 15. Jul. 2010 (UTC)
Definition (Inneres eines Dreiecks):
Das Innere eines Dreiecks  ist die Schnittmenge der drei Halbebenen
ist die Schnittmenge der drei Halbebenen 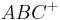 ,
, 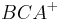 und
und 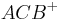 . Kurzschreibweise:
. Kurzschreibweise: 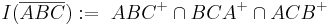
vorangegangene Diskussion
1) = g
= g
gC 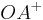 := {P| Punkt, der links von g liegt}
:= {P| Punkt, der links von g liegt}
--Nicola 13:48, 6. Jun. 2010 (UTC)
2): sei ein Dreieck und
sei ein Dreieck und 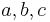 drei Geraden mit
drei Geraden mit 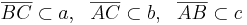 . Die Punktmenge
. Die Punktmenge 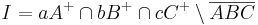 heißt das Innere des Dreiecks
heißt das Innere des Dreiecks  .
.
- --Sternchen 17:20, 10. Jun. 2010 (UTC)
Kommentar --*m.g.* 22:03, 29. Jun. 2010 (UTC)
Die Definition ist völlig korrekt. Ob man die Dreiecksseiten selbst mit zum Inneren des Dreiecks rechnet oder besser nicht, ist Ansichtssache. Sie möchten sie nicht zum Inneren rechnen. Das bleibt Ihnen unbenommen. Weil ich wegen diverser zukünftiger Beweisführungen gerne hätte, dass zum Inneren eines Winkels auch seine Schenkel gehören, würde ich persönlich bevorzugen, wenn die Dreicksseiten auch zum Inneren des Dreiecks gehören. Das braucht Sie aber nicht zu stören. Sie werden bei meinen zukünftigen Beweisen (etwa das was sich im Dunstkreis des schwachen Außenwinkelsatzes abspielen wird) sicherlich erkennen, dass ich nur aus Gründen von Formulierungsfaulheiten die Schenkel eines Winkels gern zu seinem Inneren (und damit auch die Dreiecksseiten zum Inneren eines Dreiecks) rechnen möchte.
3)Gegeben seien drei nicht kollineare Punkte A, B und C. Die Schnittmenge der offenen Halbebenen ACB+, BCA+ und ABC+ heißt das Innere des Dreiecks  .
.
Kommentar --*m.g.* 22:17, 29. Jun. 2010 (UTC)
Das ist genau so korrekt wie 2). Es wurde nur effizienter formuliert (Ob das in der momentanen Situation für die Allgemeinheit auch didaktisch effizienter ist sei dahingestellt.). Weil eine Gerade durch zwei verschiedene Punkte eindeutig bestimmt ist, kann man sie durch diese beiden Punkte auch eindeutig beschreiben. Ich glaube, dass Ihre Schreibweise für die Studierenden leichter zu verstehen ist, wenn man die Gerade  durch ein Komma von dem Referenzpunkt
durch ein Komma von dem Referenzpunkt der Halbene trennt:
der Halbene trennt: 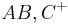 . Ob dem wirklich so ist weiß ich nicht, ich kann es mir nur vorstellen. Aber vorstellen kann man sich viel. Rückkopplung?
. Ob dem wirklich so ist weiß ich nicht, ich kann es mir nur vorstellen. Aber vorstellen kann man sich viel. Rückkopplung?

