Gruppendefinition (lang): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Definition 4*: (Gruppe, Langfassung)) |
K (→Definition 4*: (Gruppe, Langfassung)) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 15: | Zeile 15: | ||
D.h. es gilt: | D.h. es gilt: | ||
#(Abgeschlossenheit) <math>\forall a,b \in H: a \odot b \in H</math> | #(Abgeschlossenheit) <math>\forall a,b \in H: a \odot b \in H</math> | ||
| − | #(Assoziativität) <math>\forall a, b, c: (a \odot b) \odot | + | #(Assoziativität) <math>\forall a, b, c \in H: (a \odot b) \odot c = a \odot (b \odot c)</math>. |
| + | |||
==Definition 3: (Monoid)== | ==Definition 3: (Monoid)== | ||
Eine Halbgruppe <math>[M, \odot]</math> heißt Monoid, wenn sie ein Einselement hat:<br /> | Eine Halbgruppe <math>[M, \odot]</math> heißt Monoid, wenn sie ein Einselement hat:<br /> | ||
| Zeile 26: | Zeile 27: | ||
=Bemerkungen= | =Bemerkungen= | ||
==Additiv geschriebene Gruppen== | ==Additiv geschriebene Gruppen== | ||
| − | Unsere bisherigen Definitionen waren in gewisser Weise "multiplikativ" geschrieben. Bezieht man sich auf eine Struktur mit einer Operation, die eher "additiv" zu verstehen ist, spricht man häufig vom neutralen Element <math>n</math> und schreibt | + | Unsere bisherigen Definitionen waren in gewisser Weise "multiplikativ" geschrieben. Bezieht man sich auf eine Struktur mit einer Operation, die eher "additiv" zu verstehen ist, spricht man häufig vom neutralen Element <math>n</math> und schreibt die Inversen als <math>-a</math>.<br /> |
Wir geben im Folgenden die Langfassung einer Gruppendefinition, die additiv geschrieben ist und sich nicht auf bereits definierte Strukturen stützt. | Wir geben im Folgenden die Langfassung einer Gruppendefinition, die additiv geschrieben ist und sich nicht auf bereits definierte Strukturen stützt. | ||
| + | |||
==Definition 4*: (Gruppe, Langfassung)== | ==Definition 4*: (Gruppe, Langfassung)== | ||
Eine nichtleere Menge <math>G</math> zusammen mit einer Verknüpfung <math>\oplus</math> heißt Gruppe, wenn gilt: | Eine nichtleere Menge <math>G</math> zusammen mit einer Verknüpfung <math>\oplus</math> heißt Gruppe, wenn gilt: | ||
# <math>\oplus</math> ist abgeschlossen auf <math>G</math>: <math>\forall a, b \in G: a \oplus b \in G</math> | # <math>\oplus</math> ist abgeschlossen auf <math>G</math>: <math>\forall a, b \in G: a \oplus b \in G</math> | ||
| − | # <math>\oplus</math> ist assoziativ auf <math>G</math>: <math>\forall a, b, c: (a \oplus b) \oplus | + | # <math>\oplus</math> ist assoziativ auf <math>G</math>: <math>\forall a, b, c \in G: (a \oplus b) \oplus c = a \oplus (b \oplus c)</math> |
# Es gibt in <math>G</math> bzgl. <math>\oplus</math> ein neutrales Element <math>n</math>: <math>\exists n \in G \forall a \in G: a \oplus n = n \oplus a = a</math> | # Es gibt in <math>G</math> bzgl. <math>\oplus</math> ein neutrales Element <math>n</math>: <math>\exists n \in G \forall a \in G: a \oplus n = n \oplus a = a</math> | ||
# Jedes Element aus <math>G</math> hat in <math>G</math> ein inverses Element bzgl. <math>\oplus</math>: <math>\forall a \in G \exists -a \in G: a \oplus -a=-a \oplus a= n</math>. | # Jedes Element aus <math>G</math> hat in <math>G</math> ein inverses Element bzgl. <math>\oplus</math>: <math>\forall a \in G \exists -a \in G: a \oplus -a=-a \oplus a= n</math>. | ||
Aktuelle Version vom 9. Juli 2018, 12:27 Uhr
DefinitionenDefinition 1: (Algebraische Struktur)Eine Menge Schreibweise: Definition 2: (Halbgruppe)Eine algebraische Struktur
Definition 3: (Monoid)Eine Halbgruppe
Definition 4: (Gruppe)Ein Monoid
Definition 5: (Abelsche Gruppe)Wenn in einer Gruppe BemerkungenAdditiv geschriebene GruppenUnsere bisherigen Definitionen waren in gewisser Weise "multiplikativ" geschrieben. Bezieht man sich auf eine Struktur mit einer Operation, die eher "additiv" zu verstehen ist, spricht man häufig vom neutralen Element Definition 4*: (Gruppe, Langfassung)Eine nichtleere Menge
|
 zusammen mit einer Operation
zusammen mit einer Operation 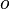 oder Relation
oder Relation  auf dieser Menge nennt man algebraische Struktur.
auf dieser Menge nennt man algebraische Struktur. ![[S, o]](/images/math/8/2/2/8222873ff784df1f8e8e2e6ac14800d4.png) bzw
bzw ![[S, r]](/images/math/8/9/e/89ec8cf7ec3eaea8e94ef96163bb1340.png)
![[H, \odot]](/images/math/b/5/0/b5051dd155dce8001fa2c6d3eec0868f.png) heißt Halbgruppe, wenn
heißt Halbgruppe, wenn
 auf
auf 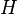 abgeschlossen und assoziativ ist.
abgeschlossen und assoziativ ist.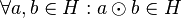
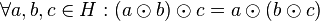 .
.
![[M, \odot]](/images/math/1/b/7/1b76d279ea0a66347bff1d26e034943a.png) heißt Monoid, wenn sie ein Einselement hat:
heißt Monoid, wenn sie ein Einselement hat: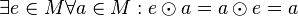
![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) heißt Gruppe, wenn jedes Element von
heißt Gruppe, wenn jedes Element von  in
in 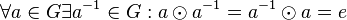
 und
und 
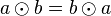 gilt, dann heißt
gilt, dann heißt  und schreibt die Inversen als
und schreibt die Inversen als 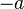 .
. heißt Gruppe, wenn gilt:
heißt Gruppe, wenn gilt:
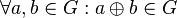
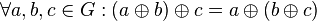
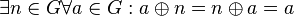
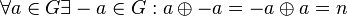 .
.

