Natürliche Zahlen mit Multiplikation: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Wir überprüfen ob es sich bei <math>[\N,\sdot]</math> um eine Gruppe handelt: (1) Abgeschlossenheit Beispiel: <math> a=4, b=5, a \sdot b=4 \sdot 5=20 \in …“) |
K |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 12: | Zeile 12: | ||
(3) neutrales Element | (3) neutrales Element | ||
| − | Beispiel: <math> a=4, | + | Beispiel: <math> a=4, e=1, a \sdot e=4 \sdot 1=4, e \in \N </math> <span style="color:green;">passt.</span> |
(4) inverses Element | (4) inverses Element | ||
| − | Beispiel: <math> a=4, a</math><sup>-1</sup><math>=(1/4), a \sdot a</math><sup>-1</sup><math>=4 \sdot (1/4)= | + | Beispiel: <math> a=4, a</math><sup>-1</sup><math>=(1/4), a \sdot a</math><sup>-1</sup><math>=4 \sdot (1/4)=1=e, a</math><sup>-1</sup><math> \notin \N </math> <span style="color:red;">passt nicht!</span> |
Somit handelt es sich bei <math>[\N,\sdot]</math> nicht um eine Gruppe. | Somit handelt es sich bei <math>[\N,\sdot]</math> nicht um eine Gruppe. | ||
Aktuelle Version vom 9. Juli 2018, 18:37 Uhr
Wir überprüfen ob es sich bei ![[\N,\sdot]](/images/math/0/3/6/0365b572ebd0ea6b7fb71b9b63d0e8da.png) um eine Gruppe handelt:
um eine Gruppe handelt:
(1) Abgeschlossenheit
Beispiel: 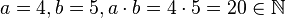 passt.
passt.
(2) Assoziativität
Beispiel: 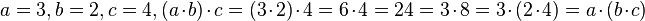 passt.
passt.
(3) neutrales Element
Beispiel: 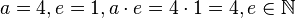 passt.
passt.
(4) inverses Element
Beispiel: 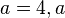 -1
-1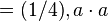 -1
-1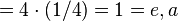 -1
-1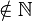 passt nicht!
passt nicht!
Somit handelt es sich bei ![[\N,\sdot]](/images/math/0/3/6/0365b572ebd0ea6b7fb71b9b63d0e8da.png) nicht um eine Gruppe.
nicht um eine Gruppe.

