Lösung von Zusatzaufgabe 8.1P (WS 18 19): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Nachstehende Abbildung zeigt den Schnitt durch einen Lichtwellenleiter (LWL) und den Weg, den ein Laserstrahl bis zum Punkt ''P'' zurücklegt (Pfeile). Das Las…“) |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
[[Datei:lwl.jpg|500px]] | [[Datei:lwl.jpg|500px]] | ||
| + | <br /> | ||
| + | [[Datei:Aufgabe 8.1 Zusatz WS 18 19.jpg|200px]]<br /> | ||
| + | 1. Kreis um P mit Radius <math>\overline{PS2}</math>, beim Schnittpunkt mit <math>\overline{CD}</math> liegt der Punk S3.<br /> | ||
| + | Option a) beim Schnittpunkt mit <math>\overline{BC}</math> liegt der Punk S4. <math>\overline{PS3}</math> und <math>\overline{S3S4}</math> konstruieren.<br /> | ||
| + | Option b) um S2 und S3 jeweils einen Kreis mit Radius <math>\overline{PS2}</math> konstruieren, der (neue) Schnittpunkt ist der Punkt P' (Spiegelung). <math>PS3^+</math> konstruieren.<br /> | ||
| + | <math>PS3^+</math> trifft in S4 auf <math>\overline{BC}</math>.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 11:50, 7. Dez. 2018 (CET) | ||
| − | + | es gibt noch eine zweite Lösung. Welche?--[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 12:03, 10. Dez. 2018 (CET) | |
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Aktuelle Version vom 10. Dezember 2018, 12:03 Uhr
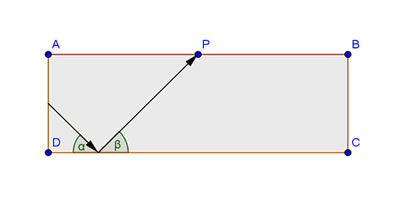
Nachstehende Abbildung zeigt den Schnitt durch einen Lichtwellenleiter (LWL) und den Weg, den ein Laserstrahl bis zum Punkt P zurücklegt (Pfeile). Das Laserlicht im LWL wird jeweils an den Grenzflächen (Glas, Luft) total reflektiert. Die beiden Grenzgeraden AB und CD können als ideale Spiegel betrachtet werden. Konstruieren Sie nur mit Zirkel und Lineal den weiteren Weg des Lichts vom Punkt P aus bis zur Begrenzungslinie 
.
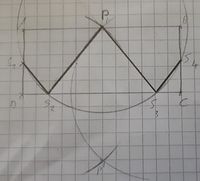
1. Kreis um P mit Radius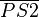 
, beim Schnittpunkt mit 
liegt der Punk S3.
Option a) beim Schnittpunkt mit liegt der Punk S4. 
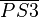und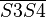 
konstruieren.
Option b) um S2 und S3 jeweils einen Kreis mit Radius 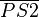konstruieren, der (neue) Schnittpunkt ist der Punkt P' (Spiegelung). 
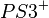konstruieren.
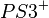trifft in S4 auf .--CIG UA (Diskussion) 11:50, 7. Dez. 2018 (CET)
es gibt noch eine zweite Lösung. Welche?--Schnirch (Diskussion) 12:03, 10. Dez. 2018 (CET)
