Lösung von Aufgabe 8.4P (WS 18 19): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Auf einem neu anzulegenden Abenteuerspielplatz steht ein senkrecht nach oben ragender Baum (Strecke <math>\overline{AB}</math> ). Dieser soll an einer Stelle '…“) |
CIG UA (Diskussion | Beiträge) |
||
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
| + | [[Datei:Aufgabe 8.4.png|400px]]<br /> | ||
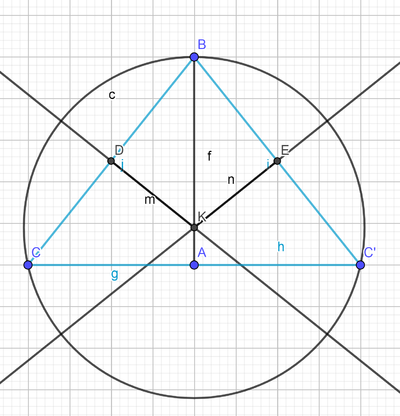
| + | 1. <math>C</math> an <math>\overline{AB}</math> spiegeln.<br /> | ||
| + | 2. Die Punkte zum Dreieck <math>\overline{BCC'}</math> verbinden.<br /> | ||
| + | 3. Mittelsenkrechte von <math>\overline{BC}</math> oder <math>\overline{BC'}</math> konstruieren<br /> | ||
| + | => Der Schnittpunkt ist K.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 21:51, 6. Dez. 2018 (CET) | ||
| + | |||
| + | super, das passt. Können Sie auch erklären, warum diese Konstruktion zum Ziel führt?--[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 10:07, 10. Dez. 2018 (CET) | ||
| + | |||
| + | Gesucht wurde ja der Kreismittelpunkt des gestrichelten Kreises der Skizze. Da jedes Dreieck einen Umkreis besitzt, und durch Spiegelung an AB hier ein gleichschenkliges Dreieck entsteht, bei denen der Umkreismittelpunkt auf der Mittelsenkrechten der Basis liegt (weil C und C' den gleichen Abstand dazu haben => Aufgabe 9.5), kann man über die oben beschriebene Konstruktion K bestimmten und den Umkreis konstruieren.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 11:07, 14. Dez. 2018 (CET) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Aktuelle Version vom 14. Dezember 2018, 11:07 Uhr
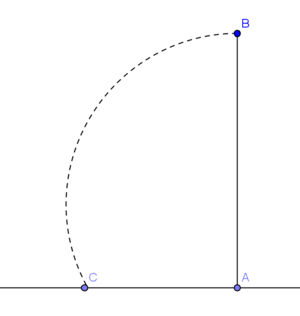
Auf einem neu anzulegenden Abenteuerspielplatz steht ein senkrecht nach oben ragender Baum (Strecke 
). Dieser soll an einer Stelle K so angesägt werden, dass er hier umknickt und mit seiner Spitze an einer Stelle C am Boden zu liegen kommt (siehe Skizze). Konstruieren Sie die Knickstelle K.
1. 
an spiegeln.
2. Die Punkte zum Dreieck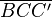 
verbinden.
3. Mittelsenkrechte von 
oder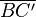 
konstruieren
=> Der Schnittpunkt ist K.--CIG UA (Diskussion) 21:51, 6. Dez. 2018 (CET)
super, das passt. Können Sie auch erklären, warum diese Konstruktion zum Ziel führt?--Schnirch (Diskussion) 10:07, 10. Dez. 2018 (CET)
Gesucht wurde ja der Kreismittelpunkt des gestrichelten Kreises der Skizze. Da jedes Dreieck einen Umkreis besitzt, und durch Spiegelung an AB hier ein gleichschenkliges Dreieck entsteht, bei denen der Umkreismittelpunkt auf der Mittelsenkrechten der Basis liegt (weil C und C' den gleichen Abstand dazu haben => Aufgabe 9.5), kann man über die oben beschriebene Konstruktion K bestimmten und den Umkreis konstruieren.--CIG UA (Diskussion) 11:07, 14. Dez. 2018 (CET)
