Lösung von Aufgabe 8.3P (WS 18 19): Unterschied zwischen den Versionen
CIG UA (Diskussion | Beiträge) |
CIG UA (Diskussion | Beiträge) |
||
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
3. <math>\overline{AP'}</math> konstruieren, mit dem Schnittpunkt S1 <math>\overline{S1B'}</math> konstruieren, abschließend <math>\overline{S2B'}</math>.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 11:30, 7. Dez. 2018 (CET) | 3. <math>\overline{AP'}</math> konstruieren, mit dem Schnittpunkt S1 <math>\overline{S1B'}</math> konstruieren, abschließend <math>\overline{S2B'}</math>.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 11:30, 7. Dez. 2018 (CET) | ||
| + | auch eine schöne Lösung! -Erklärung?--[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 11:58, 10. Dez. 2018 (CET) | ||
| + | |||
| + | Da A und B den gleichen Abstand zu P haben ist die Verbindung jeweils eines Punktes zu P (die kürzeste über die jeweilige Bande) auch gleichzeitig vom Betrag und von den Winkeln gleich der anderen. Bzw: Wenn wir P als Spiegelpunkt nehmen, dann wird A-S1-P auf P-S2-B abgebildet und andersherum.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 11:14, 14. Dez. 2018 (CET) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Aktuelle Version vom 14. Dezember 2018, 11:14 Uhr
Die nachfolgende GeoGebra-Applikation zeigt einen Billardtisch mit zwei Kugeln in der Draufsicht. Kugel A soll durch einen zentralen Stoß die Kugel B über zwei Banden treffen. Konstruieren und Begründen Sie Ihre Konstruktion.
Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren.
_%E2%80%93_Geometrie-Wiki.png)
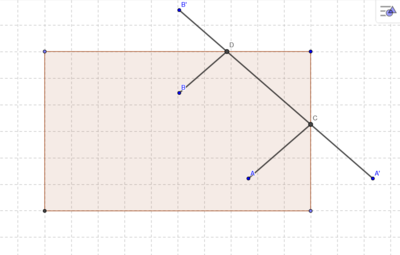
Betrag(Strecke AB) ist der kürzeste Weg von A über Bande (rechts) und Bande (oben) zu B. Def (Strecke)-Azalea (Diskussion) 18:22, 6. Dez. 2018 (CET)
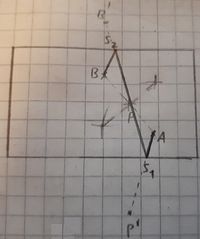
1. Mittelpunkt von 
konstruieren.
2. P an der Unterkante spiegeln, B an der Oberkante spiegeln.
3. 
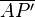konstruieren, mit dem Schnittpunkt S1 
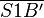konstruieren, abschließend 
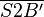.--CIG UA (Diskussion) 11:30, 7. Dez. 2018 (CET)
auch eine schöne Lösung! -Erklärung?--Schnirch (Diskussion) 11:58, 10. Dez. 2018 (CET)
Da A und B den gleichen Abstand zu P haben ist die Verbindung jeweils eines Punktes zu P (die kürzeste über die jeweilige Bande) auch gleichzeitig vom Betrag und von den Winkeln gleich der anderen. Bzw: Wenn wir P als Spiegelpunkt nehmen, dann wird A-S1-P auf P-S2-B abgebildet und andersherum.--CIG UA (Diskussion) 11:14, 14. Dez. 2018 (CET)
