Lösung von Aufgabe 10.2P (WS 18/19): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie Satz IX.2:<br /> Gegeben seien zwei Spiegelgeraden ''a'' und ''b'' mit einem gemeinsamen Schnittpunkt ''S'', sowie zwei Punkten <math>A\in a</math…“) |
CIG UA (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie Satz IX.2:<br /> | Beweisen Sie Satz IX.2:<br /> | ||
Gegeben seien zwei Spiegelgeraden ''a'' und ''b'' mit einem gemeinsamen Schnittpunkt ''S'', sowie zwei Punkten <math>A\in a</math> und <math>B\in b</math>, die von ''S'' jeweils verschieden sind. Wir betrachten die Verkettung <math>S_{a}\circ S_{b} </math>. Für einen beliebigen Punkt P und seinen Bildpunkt <math>P''=S_{a}\circ S_{b}(P) </math> gilt: <math>\left| \angle PSP'' \right| =2\cdot\left| \angle ASB \right|</math>.<br /> | Gegeben seien zwei Spiegelgeraden ''a'' und ''b'' mit einem gemeinsamen Schnittpunkt ''S'', sowie zwei Punkten <math>A\in a</math> und <math>B\in b</math>, die von ''S'' jeweils verschieden sind. Wir betrachten die Verkettung <math>S_{a}\circ S_{b} </math>. Für einen beliebigen Punkt P und seinen Bildpunkt <math>P''=S_{a}\circ S_{b}(P) </math> gilt: <math>\left| \angle PSP'' \right| =2\cdot\left| \angle ASB \right|</math>.<br /> | ||
| − | + | <br /> | |
| + | Vor: P''= S<sub>a</sub><math>\circ</math>S<sub>b</sub>(P). Beh: |<(PSP'')|= 2|<(ASB)|<br /> | ||
| + | 1.) S<sub>a</sub>(P) = P' und S<sub>b</sub>(P') = P'' '''- Vor., Verkettung von Geradenspiegelung'''<br /> | ||
| + | 2.) <math>|\angle PSA| = |\angle P'SA|</math> '''- 1.) Winkelmaßerhaltung'''<br /> | ||
| + | 3.) <math>|\angle P'SB| = |\angle P''SB|</math> '''- 1.) Winkelmaßerhaltung'''<br /> | ||
| + | 4.) <math>|\angle PSP'| = |\angle PSA|+|\angle ASP'| = 2|\angle PSA|</math> '''- 2.), Winkeladdition'''<br /> | ||
| + | 5.) <math>|\angle P'SP''| = |\angle P'SB|+|\angle BSP''| = 2\angle P''SB|</math> '''- 3.), Winkeladdition'''<br /> | ||
| + | 6.) <math>|\angle PSP''| = |\angle PSP'|+|\angle P'SP''|</math> '''- Winkeladdition'''<br /> | ||
| + | 7.) <math>|\angle PSP''| = 2|\angle PSA|+ 2|\angle P''SB|</math> '''- 4.), 5.), 6.)'''<br /> | ||
| + | 8.) <math>|\angle PSP''| = 2( |\angle ASP'|+|\angle P'SB|</math> ) '''- 7.), Distributivgesetz'''<br /> | ||
| + | 9.) <math>|\angle PSP''| = 2( |\angle ASB| )</math> '''- 8.) Winkeladdition'''<br /> | ||
| + | => <math>|\angle PSP''|= 2|\angle ASB|</math>. Die Behauptung ist damit bewiesen.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 21:35, 20. Dez. 2018 (CET) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Version vom 20. Dezember 2018, 21:35 Uhr
Beweisen Sie Satz IX.2:
Gegeben seien zwei Spiegelgeraden a und b mit einem gemeinsamen Schnittpunkt S, sowie zwei Punkten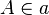 
und 
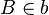, die von S jeweils verschieden sind. Wir betrachten die Verkettung 
. Für einen beliebigen Punkt P und seinen Bildpunkt 
gilt: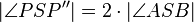 
.
Vor: P= Sa
Sb(P). Beh: |<(PSP)|= 2|<(ASB)|
1.) Sa(P) = P' und Sb(P') = P - Vor., Verkettung von Geradenspiegelung
2.) 
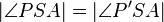- 1.) Winkelmaßerhaltung
3.) 
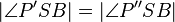- 1.) Winkelmaßerhaltung
4.) 
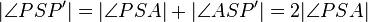- 2.), Winkeladdition
5.) 
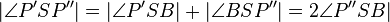- 3.), Winkeladdition
6.) 
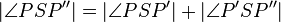- Winkeladdition
7.) 
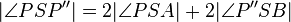- 4.), 5.), 6.)
8.) 
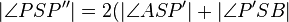) - 7.), Distributivgesetz
9.) 
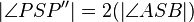- 8.) Winkeladdition
=> 
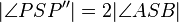. Die Behauptung ist damit bewiesen.--CIG UA (Diskussion) 21:35, 20. Dez. 2018 (CET)
