Übungsaufgaben zur Algebra, Serie 1 SoSe 2019: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#CCFFCC; align:left;"> {|width=90%| style="backgro…“) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 02) |
||
| Zeile 7: | Zeile 7: | ||
Es sei <math>M_{2\times2}</math> die Menge aller <math>2 \times 2-</math>Matrizen. Beweisen Sie:<br /> | Es sei <math>M_{2\times2}</math> die Menge aller <math>2 \times 2-</math>Matrizen. Beweisen Sie:<br /> | ||
<math>\exists E \in M_{2\times2}\forall M \in M_{2\times2} : E \cdot M=M\cdot E= M</math>. | <math>\exists E \in M_{2\times2}\forall M \in M_{2\times2} : E \cdot M=M\cdot E= M</math>. | ||
| − | + | =Aufgabe 03= | |
| + | Geben Sie <math>10</math> Nullteiler aus <math>M_{2\times2}</math> an. | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Algebra]] | [[Kategorie:Algebra]] | ||
Version vom 14. Mai 2019, 13:02 Uhr
Aufgabe 01Beweisen Sie: Die natürlichen Zahlen bilden sowohl bzgl. der Addition als auch bezüglich der Multiplikation keine Gruppe. Aufgabe 02Es sei Aufgabe 03Geben Sie |
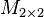die Menge aller 
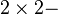Matrizen. Beweisen Sie:
.
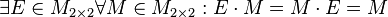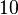Nullteiler aus 
