Übungsaufgaben zur Algebra, Serie 1 SoSe 2019: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 02)
(→‎Aufgabe 03)
Zeile 9: Zeile 9:
 
=Aufgabe 03=
 
=Aufgabe 03=
 
Geben Sie <math>10</math> Nullteiler aus <math>M_{2\times2}</math> an.
 
Geben Sie <math>10</math> Nullteiler aus <math>M_{2\times2}</math> an.
 +
=Aufgabe 04=
 +
Es sei <math>D_{45}:= \begin{pmatrix} \frac{1}{2}\sqrt{2} & -\frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \end{pmatrix}</math>. Ergänzen Sie <math>D:=\{D_{45}, \ldots\}</math> derart, dass <math>[D, \cdot]</math> eine Gruppe ist.
 +
=Aufgabe 05=
 +
Beweisen Sie: <br />
 +
Die Matrix <math>\begin{pmatrix} 1 & 2 \\ 2 & 4 \end{pmatrix}</math> ist nicht invertierbar.
 +
=Aufgabe 06=
 +
<math>A:=\begin{pmatrix} a & b \\ c & d \end{pmatrix}</math><br />
 +
 +
Wir definieren die Determinante <math>det(A)</math> wie folgt:<br />
 +
<math>det(A):=|A|:=a \cdot d - b \cdot c</math><br />
 +
Beweisen Sie: Die Matrizenmultiplikation ist abgeschlossen auf der Menge aller <math>2\times2-</math>Matrizen, deren Determinate 1 ist.
 +
=Aufgabe 07=
 +
 +
 
<!--- Was hier drunter steht muss stehen bleiben --->
 
<!--- Was hier drunter steht muss stehen bleiben --->
 
|}
 
|}
 
</div>
 
</div>
 
[[Kategorie:Algebra]]
 
[[Kategorie:Algebra]]

Version vom 14. Mai 2019, 13:53 Uhr

Inhaltsverzeichnis

Aufgabe 01

Beweisen Sie: Die natürlichen Zahlen bilden sowohl bzgl. der Addition als auch bezüglich der Multiplikation keine Gruppe.

Aufgabe 02

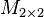Es sei M_{2\times2} die Menge aller 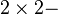2 \times 2-Matrizen. Beweisen Sie:
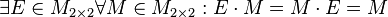\exists E \in M_{2\times2}\forall M \in M_{2\times2} : E \cdot M=M\cdot E= M.

Aufgabe 03

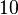Geben Sie 10 Nullteiler aus M_{2\times2} an.

Aufgabe 04

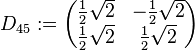Es sei D_{45}:= \begin{pmatrix} \frac{1}{2}\sqrt{2} & -\frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \end{pmatrix}. Ergänzen Sie 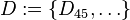D:=\{D_{45}, \ldots\} derart, dass [D, \cdot] eine Gruppe ist.

Aufgabe 05

Beweisen Sie:
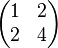Die Matrix \begin{pmatrix} 1 & 2 \\ 2 & 4 \end{pmatrix} ist nicht invertierbar.

Aufgabe 06

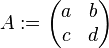
A:=\begin{pmatrix} a & b \\ c & d \end{pmatrix}

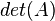Wir definieren die Determinante det(A) wie folgt:
det(A):=|A|:=a \cdot d - b \cdot c
Beweisen Sie: Die Matrizenmultiplikation ist abgeschlossen auf der Menge aller 2\times2-Matrizen, deren Determinate 1 ist.

Aufgabe 07

Von „http://geometrie.zum.de/index.php?title=Übungsaufgaben_zur_Algebra,_Serie_1_SoSe_2019&oldid=33125“