Gruppendefinition (kurz): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#CCFFCC; align:left;"> {|width=90%| style="backgro…“) |
K (→Beweis von Satz 1) |
||
| (9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{|width=90%| style="background-color:#CCFFCC; padding:1em" | {|width=90%| style="background-color:#CCFFCC; padding:1em" | ||
| valign="top" | | | valign="top" | | ||
| + | =Linksinvers gleich Rechtsinvers= | ||
| + | ==Satz 1== | ||
| + | Es sei <math>[G, \odot]</math> eine Gruppe.<br /> | ||
| + | <math>\forall a \in G: a \odot b = e \land c \odot a = e \Rightarrow b=c</math> | ||
| + | ==Beweis von Satz 1== | ||
| + | Es sei <math>b</math> das Linksinverse bzgl. <math>\odot</math> von <math>a</math>. Also <math>b\odot a = e</math> ist unsere Voraussetzung.<br /> | ||
| + | Wir multiplizieren <math>b</math> von rechts mit <math>a</math>: | ||
| + | {| | ||
| + | |- | ||
| + | | (I)|| <math>a \odot b = e \odot a \odot b </math>|| (Wir haben <math>a</math> mit <math>b</math> von rechts multipliziert | ||
| + | |- | ||
| + | | (II) || <math>a \odot b = (b^{-1} \odot b)\odot a \odot b </math> ||(Auch <math>b</math> hat ein Linksinverses <math>b^{-1}</math> | ||
| + | |- | ||
| + | |(III) || <math>a \odot b = b^{-1} \odot (b\odot a) \odot b </math> || (Assoziativität) | ||
| + | |- | ||
| + | |(IV) || <math>a \odot b = b^{-1} \odot e \odot b </math> || (<math>b</math> ist das Linksinverse von <math>a</math>) | ||
| + | |- | ||
| + | | (V) || <math>a \odot b = b^{-1} \odot b </math> || (Eigenschaften des Einselements) | ||
| + | |- | ||
| + | | (VI) || <math>a \odot b = e </math> || (<math>b^{-1}</math> ist das Linksinverse von <math>b</math> | ||
| + | |} | ||
| + | Mit Gleichung (VI) haben wir gezeigt, dass das Linksinverse von <math>a</math> auch Rechtsinverses von <math>a</math> ist. | ||
| − | + | =Linkseins gleich Rechtseins= | |
| − | + | ==Satz 2== | |
| + | Es sei <math>[G, \otimes]</math> eine Gruppe. Wenn <math>e \in G</math> von links multipliziert Einselement von <math>[G, \otimes]</math> ist, dann ist <math>e</math> auch von rechts multipliziert Einselement von <math>G</math>. | ||
| + | ==Beweis von Satz 2== | ||
| + | Es sei <math>[G, \otimes]</math> Gruppe. Es gelte ferner für das Element <math>e \in G</math> die folgende Eigenschaft: <math>\forall g \in G: e \otimes g = g</math>.<br /> | ||
| + | Wir haben zu zeigen, dass jetzt auch <math>g \otimes e = g</math> für alle <math>g</math> aus <math>G</math> gilt.<br /> | ||
| + | Wir gehen von <math>(I) e \otimes g = g</math>.<br /> | ||
| + | In Gleichung <math>(I)</math> multiplizieren wir von rechts auf beiden Seiten mit <math>g^{-1}\otimes g</math> und erhalten <math>(II)</math>.<br /> | ||
| + | <math>(II) e \otimes g \otimes (g^{-1}\otimes g) = g \otimes (g^{-1}\otimes g)</math>.<br /> | ||
| + | Aus <math>(II)</math> folgt:<br /> | ||
| + | <math>(III) e \otimes g = g \otimes e</math> q,e.d. | ||
| + | =Verkürzte Gruppendefinition= | ||
| + | Wegen der Gültigkeit von Satz 1 und Satz 2 können wir unsere Gruppendefinition kürzer schreiben: | ||
| + | ==Definition 5: Gruppe (verkürzte Schreibweise)== | ||
| + | Eine nichtleere Menge <math>G</math> zusammen mit einer Verknüpfung <math>\oplus</math> heißt Gruppe, wenn gilt: | ||
| + | # <math>\oplus</math> ist abgeschlossen auf <math>G</math>: <math>\forall a, b \in G: a \oplus b \in G</math> | ||
| + | # <math>\oplus</math> ist assoziativ auf <math>G</math>: <math>\forall a, b, c \in G: (a \oplus b) \oplus c = a \oplus (b \oplus c)</math> | ||
| + | # Es gibt in <math>G</math> bzgl. <math>\oplus</math> ein neutrales Element <math>n</math>: <math>\exists n \in G \forall a \in G: a \oplus n = a</math> | ||
| + | # Jedes Element aus <math>G</math> hat in <math>G</math> ein inverses Element bzgl. <math>\oplus</math>: <math>\forall a \in G \exists -a \in G: a \oplus -a= n</math>. | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Algebra]] | [[Kategorie:Algebra]] | ||
Aktuelle Version vom 27. Mai 2019, 12:32 Uhr
Linksinvers gleich RechtsinversSatz 1Es sei Beweis von Satz 1Es sei
Mit Gleichung (VI) haben wir gezeigt, dass das Linksinverse von Linkseins gleich RechtseinsSatz 2Es sei Beweis von Satz 2Es sei Verkürzte GruppendefinitionWegen der Gültigkeit von Satz 1 und Satz 2 können wir unsere Gruppendefinition kürzer schreiben: Definition 5: Gruppe (verkürzte Schreibweise)Eine nichtleere Menge
|
![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe.
eine Gruppe.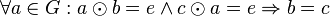
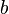 das Linksinverse bzgl.
das Linksinverse bzgl.  von
von  . Also
. Also 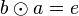 ist unsere Voraussetzung.
ist unsere Voraussetzung.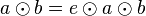

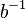

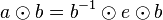
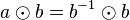
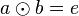
![[G, \otimes]](/images/math/0/1/3/01322720752789c5d9651172aee2d990.png) eine Gruppe. Wenn
eine Gruppe. Wenn  von links multipliziert Einselement von
von links multipliziert Einselement von  auch von rechts multipliziert Einselement von
auch von rechts multipliziert Einselement von  .
.
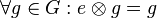 .
.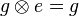 für alle
für alle  aus
aus 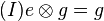 .
.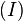 multiplizieren wir von rechts auf beiden Seiten mit
multiplizieren wir von rechts auf beiden Seiten mit 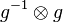 und erhalten
und erhalten 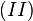 .
.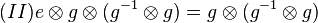 .
.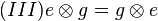 q,e.d.
q,e.d.
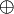 heißt Gruppe, wenn gilt:
heißt Gruppe, wenn gilt:
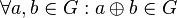
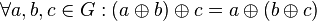
 :
: 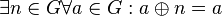
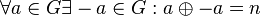 .
.

