GeometrieUndUnterrichtSS2019 07: Unterschied zwischen den Versionen
(→Ergebnisse der Nachbereitung) |
(→Ergebnisse der Nachbereitung) |
||
| Zeile 88: | Zeile 88: | ||
*Wo liegen die größten Hürden beim Lösen des Problems für SuS? Wie kann ihnen beim Problemlösen geholfen werden? | *Wo liegen die größten Hürden beim Lösen des Problems für SuS? Wie kann ihnen beim Problemlösen geholfen werden? | ||
|| | || | ||
| − | *Da eine Problem nur von dem Problemlösenden zu einem solchen erkoren werden kann, ist der Kenntnisstand des Problemlösenden der entscheidende Faktor zur Problemidentifizierung. So erachte ich die Aufgabe für SuS der 7. Klasse durchaus als eine recht anspruchsvolle Problemstellung. Das Problem lässt sich so wie es oben formuliert wurde der Kategorie Existenzproblem/Anzahlproblem zuordnen, doch | + | *Da eine Problem nur von dem Problemlösenden zu einem solchen erkoren werden kann, ist der Kenntnisstand des Problemlösenden der entscheidende Faktor zur Problemidentifizierung. So erachte ich die Aufgabe für SuS der 7. Klasse durchaus als eine recht anspruchsvolle Problemstellung. Das Problem lässt sich so wie es oben formuliert wurde der Kategorie Existenzproblem/Anzahlproblem zuordnen, doch lässt es sich sicherlich auch als von Beweis- und Konstruktionsproblem formulieren. Weiterhin gibt es Optimierungs-, Modellierungs- und Berechnungsprobleme. |
| − | *Zunächst einmal muss das '''Problem verstanden''' und durchdrungen werden. Bekannt sind der Gegenstand, nämlich Dreiecke, sowie Bedingungen für die Winkel des Dreiecks, wobei die Bedingung a priori nicht ausreicht um alle Winkel zu bestimmen (3 Unbekannte, 1 Gleichung). Beim '''Entwickeln eines Lösungsplans''' liegt es nahe zunächst einmal zu Rekapitulieren, welche Regeln/Formeln/Verfahren/Sätze in dem Kontext „Dreieck und Winkel im Dreieck“ bekannt sind. Hierzu zählen in Klasse 7 der Satz von der Winkelsumme im Dreieck, der Satz des Gleichschenkligen Dreiecks und der Satz des Thales. Außerdem | + | *Zunächst einmal muss das '''Problem verstanden''' und durchdrungen werden. Bekannt sind der Gegenstand, nämlich Dreiecke, sowie Bedingungen für die Winkel des Dreiecks, wobei die Bedingung a priori nicht ausreicht um alle Winkel zu bestimmen (3 Unbekannte, 1 Gleichung). Für geübte Gleichungssystemanwender ergibt sich durch die Analyse schon der Hinweis eine zweite Bestimmungsgleichung zu finden. <br /> |
| − | + | :Beim '''Entwickeln eines Lösungsplans''' liegt es nahe zunächst einmal zu Rekapitulieren, welche Regeln/Formeln/Verfahren/Sätze in dem Kontext „Dreieck und Winkel im Dreieck“ bekannt sind. Hierzu zählen in Klasse 7 beispielsweise der Satz von der Winkelsumme im Dreieck, der Satz des Gleichschenkligen Dreiecks und der Satz des Thales. Außerdem ist es sinnvoll beim Annähern an einen Lösungsweg heuristischen Strategien wie das konkret-experimentelles Lösen und das Spezialisieren des Problems zu verwenden, um Protyp-Dreiecke z.B. gleichschenkliche, gleichseitige oder rechtwinklige Dreiecke auf die Bedingung zu testen. Dadurch wird min. ein Dreieck gefunden, d.h. die Existenz bewiesen, und noch dazu die Vermutung, dass alle rechtwinklige Dreiecke die Bedinung erfüllen, gewonnen. Für die Begründung dieser Vermutung ist es insbesondere wichtig das Probelm auf ein Berechnungsproblem bzw. das Lösen von einem Gleichungssystem zu reduzieren. Die zweite Gleichung für die drei Winkelvariablen erhalten wir aus dem Satz von der Winkelsumme im Dreieck:<br /> | |
| + | #<math>\alpha = \beta+\gamma </math> | ||
| + | #<math>\alpha + \beta + \gamma = 180^\circ </math> <br /> | ||
| + | :1. in 2: <math> 2(\beta+\gamma) = 180^\circ \Rightarrow \alpha = \beta + \gamma = 90^\circ </math> <br /> | ||
| + | :In der '''Rückschau''', ein nicht zu vernachlässigender Schritt des Lösungsprozesses, wird über das Problem reflektiert. So deckt sich dieser Lösungsweg inhaltlich mit dem Beweis des Satz des Thales. Außerdem ist ersichtlich, dass zur Bestimmung von <math>\beta</math> und <math>\gamma</math> noch eine weitere Bedingung/ Gleichung gestellt werden muss. Für den oben beschriebenen Lösungsweg wurde "nur" der Satz von der Winkelsumme im Dreieck und Äquivalenzumformungen gebraucht. | ||
| + | * Meiner Meinung nach können die SuS sehr schnell durch Ausprobieren auf die rechtwinklige Dreiecke kommen, doch stellt der Lösungsweg mit Hilfe von Gleichungsystemen eine große Hürde da; selbst dann noch, wenn die SuS zuvor Äquivalenzumformungen und Lösen von Gleichungssystemen trainiert haben. Das Arbeiten mit Variablen und das Einsetzen von Gleichungen muss häufig geübt werden und wird erst nach mehrjähirger Übung von den meisten SuS verstanden. Auch die Idee bei einer Geometrieaufgabe algebraische Hilfsmittel zu nutzen ist nicht intuitiv. Hier fände ich einen (optionalen) Tipp wie "Stelle zwei Gleichungen mit <math>\alpha,\beta</math> und <math>\gamma</math> auf" oder "Nutze den Satz der Winkelsumme im Dreieck" hilfreich. | ||
|| | || | ||
| − | + | Zur Beantwortung der Aufgabe sind die erlernten Problemkategorien auf ein konkrete Fragstellung anzuwenden und die Phasen des Problemlösens an dem Problem zu näher erläutern. Zuletzt wird eine didaktische Analyse des Problems gefordert. | |
<!-- === Abgabe Anna-Lena Fertig Ende ============================================================================================================ --> | <!-- === Abgabe Anna-Lena Fertig Ende ============================================================================================================ --> | ||
<!-- === Tabelle Ende ====================================================================================================================== --> | <!-- === Tabelle Ende ====================================================================================================================== --> | ||
Version vom 7. Juni 2019, 18:32 Uhr
Inhaltsverzeichnis |
Vorbereitungsauftrag
Die Schüler*in Alice und Bob haben die unten stehende Aufgabe bearbeitet.
- Bewerten Sie zunächst die jeweiligen Konstruktionsbeschreibungen der Schüler*innen. Diskutieren Sie gegebenenfalls Fehler.
- Führen Sie die Konstruktion gemäß der Konstruktionsbeschreibungen durch. Diskutieren Sie gegebenenfalls Probleme, die Ihnen bei der Durchführung auffallen.
Dreieckskonstruktion SSWk
Konstruiere ein Dreieck ABC mit den folgenden Eigenschaften: 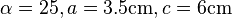 . Beschreibe deine Konstruktion.
. Beschreibe deine Konstruktion.
Konstruktionsbeschreibung von Alice (Zirkel & Lineal)
- Ich ziehe einen 6cm langen Strich. Am rechten Ende (B) steche ich den Zirkel in das Blatt und stelle ihn auf 3,5 cm ein. Jetzt zirkle ich einen Halbkreis nach oben. Dieser Halbkreis schneidet den Winkel, den ich vorher am linken Ende der Strecke mit dem Geodreieck eingezeichnet habe, in zwei Punkten. Jetzt verbinde ich die erhaltenen Punkte miteinander und sehe, dass es zwei Dreiecke gibt, die die SSWk=Konnsstruktion erfüllen.
Quelle: „Erziehen im Mathematikunterricht.“ In: Kaenders & Schmidt (Hrsg.) Mit GeoGebra mehr Mathematik verstehen.
Konstruktionsbeschreibung von Bob (GeoGebra)
- Zeichne Strecke a mit Länge 3,5cm. Zeichne Kreis um B mit Länge 6cm. Erstelle Punkt A auf dem Kreis und Messe den Winkel α = ∠BAC. Verschiebe Punkt A auf dem Kreis so, dass α = 25°. Spiegele das Dreieck ABC an a. Ich habe jetzt zwei Dreiecke, die die Bedingungen erfüllen.
Ergebnisse des Vorbereitungsauftrags
Bearbeitung von Ilona
Die Konstruktionsbeschreibung von Alice verwendet tendentiell einfachere Begriffe und vermeidet konkrete mathematische Bezeichnungen (z.B. Strich statt Strecke von A nach B). Auch folgt sie in der Beschreibung der Schritte nicht der tatsächlichen Reihenfolge, sondern springt zwischendurch zurück ("Winkel, den ich vorher...eingezeichnet habe"). Darüber hinaus bezeichnet Alice die geometrischen Objekte ihrer Konstruktion nicht eindeutig (z.B. "am linken Ende der Strecke"). Allerdings konstruiert sie zwei Dreiecke, welche die Anforderungen erfüllen, wenn auch die Formulierung "Jetzt verbinde ich die erhaltenen Punkte" wieder nicht sehr präzise ist und nur erahnen lässt, was genau dieser Schritt beinhaltet. Bob hingegen formuliert meiner Meinung nach präziser und unter Verwendung mathematischer Begriffe sein Vorgehen. Beispielsweise führt er die Benennung der Punkte, Winkel und Strecken seiner Konstruktion stringent durch. Bob hat seine Konstruktion offenbar mit Hilfe von Geogebra durchgeführt, wodurch es ihm möglich war, den Punkt A auf dem Kreis um B zu verschieben, bis der Winkel α die gewollte Größe hatte. Konstruiert man mit Zirkel und Lineal, so erweist sich dieses Vorgehen jedoch als schwierig und der Ansatz von Alice als praktikabler. Auch hat Bob durch seine Spiegelung an der durch a verlaufenden Gerade lediglich zwei Dreiecke konstruiert, die zueinander kongruent bzw. durch Verschiebung / Spiegelung / Drehung ineinander überführbar sind. Das Dreieck, welches Alice zusätzlich gefunden hat, fehlt in Bobs Konstruktion (es wurde aber auch nur die Konstruktion eines Dreiecks in der Aufgabenstellung gefordert). Die Konstruktionsbeschreibung von Alice lässt sich recht gut durchführen, wenn man die fehlenden Benennungen der geometrischen Objekte für sich erschließt. Bobs Beschreibung funktioniert gut bis zu dem Punkt, an welchem er den Punkt A auf dem Kreis verschiebt, bis der Winkel stimmt. Dieser Schritt lässt sich nur mit Hilfsmitteln wie Geogebra leicht durchführen.
Bearbeitung von Wibke
Alice’s Konstruktionsbeschreibung führt zum Ziel, jedoch ist ihre Ausdrucksweise nicht fachlich korrekt. Sie sollte folgende sprachlichen Formulierungen beachten:
Strich – Strecke von A nach B
In das Blatt – Zirkel bei B ansetzen
Zirkle Halbkreis nach oben – Zeichne Kreis um B
Schneidet Winkel – schneidet die Gerade
Linkes Ende – Punkt A
Punkte verbinden – Stecken AC, AC‘
Außerdem, sollte die Konstruktionsbeschreibung in der Reihenfolge geschrieben werden, in welcher auch die einzelnen Schritte durchgeführt werden.
Bob’s Konstruktionsbeschreibung führt ebenfalls zum Ziel. Er konstruiert mit Hilfe von Geogebra zwei kongruente Dreiecke. Falls die Aufgabenstellung nur so gegeben wird, ohne konkrete Hilfsmittel zu nennen, halte ich seine Ausführung für gut. Will man, dass die SuS mit Zirkel und Lineal arbeiten, sollte dies explizit in der Aufgabenstellung genannt werden.
Bearbeitung von Anna-Lena
Meine Vorredner haben die wichtigsten Bemerkungen zu den beiden Konstruktionsbeschreibungen schon gemacht. Diesen stimme ich zu, weshalb ich hier nur noch ergänze: Aus der Konstruktionsbeschreibung von Alice geht die Konstruktion eines zweiten Dreiecks nicht hervor, da sie nur einen Winkel in B abträgt und von einem Zweiten, nach unten Gespiegelten nie die Rede war. Die Konstruktionsbeschreibung ist deshalb meiner Meinung nach auch bei Hinwegsehen der (fach-)sprachlichen Mängel und der Reihenfolge nicht vollkommen richtig. Dennoch nennt sie die entscheidenden Konstruktionsschritte. Die Konstruktionsbschreibung zeigt auch wie wichtig das Training und auch die häufige Kontrolle der logischen Argumentationsweise sowie der korrekte Fachsprache bei den Texten der SuS ist.
Bob's Konstruktionsbeschreiben lässt sich ohne Probleme nachvollziehen. Sein Ansatz ist in dem Sinne interessant, dass sich durch die Variation der Winkelbreite eine dynamische Konstruktion entwickelt. Er kann durch den Prozess entdecken, dass die Angaben SSW bis auf Konkruenz ein solches Dreieck eindeutig bestimmen und wie sich das Dreieck beim Abändern einer Größe verändert. Darauf müssen SuS meiner Meinung bei Konstruktionen mit Zirkel und Lineal eher aufmerksam gemacht werden. Die Konstruktion des Dreieck mit Bob's Methode bedarf jedoch höchst wahrscheinlich mehrerer Schritte, s.d. das das Hilfmittel Geogebra bis auf den obenen genannten keinen Vorteil bringt.
Bei beiden Ansätzen stellt sich mir die Frage, ob die Konstruktion des zweiten Dreiecks die Aufgabe überhaupt erfüllt. Da "ein(?)" Dreieck ABC konstruiert werden sollte und nicht das Dreieck ACB.
Sitzungsmaterialien
- Begleitfolien der Sitzung vom 07.06.2019
- Arbeitsblätter zu Konstruktionsaufgaben und idealtypische Problemlöseprozesse
Dokumentation der Sitzung
Nachbereitungsauftrag
Entwerfen Sie eine Prüfungsfrage bzw. ein kurzes Prüfungsgespräch zu den Sitzungen zum Begriffslernen (I+II). Ihre Frage sollte dabei nicht nur bloße Wissensabfrage sein, sondern auch Anwendungen, Begründungen oder Diskussionen erfordern. (Sollte Ihnen doch nur Aufgaben zur bloßen Wissensabfrage einfallen, entwerfen Sie drei Prüfungsfragen.)
- Formulieren Sie Ihre Prüfungsfrage bzw. den Anlass für das Prüfungsgespräch in der Aufgabenstellung-Spalte.
- Beschreiben Sie ausführlich, wie mögliche (richtige) Antworten auf Ihre Frage aussehen könnten bzw. welche Aspekte in einem Prüfungsgespräch zu dieser Frage angesprochen werden sollten. Tragen Sie dies entsprechend in die Erwartungshorizont-Spalte ein.
- Erläutern Sie kurz, warum Sie diese Aufgabe einen zentralen Aspekt der Sitzung abdeckt und welche Anforderung an Wissen/Kompetenzen die Aufgabe fordert.
Unter den übergreifenden Literaturhinweise sind insbesondere relevant:
- „Erziehen im Mathematikunterricht.“ In: Kaenders & Schmidt (Hrsg.) Mit GeoGebra mehr Mathematik verstehen.
- Kapitel 3 „Konstruieren“ in Weigand et. al. (2018). „Didaktik der Geometrie für die Sekundarstufe I“
- Präsentationsfolien zu Kapitel 3 „Konstruieren“ der Vorlesung „Didaktik der Mathematik in der Sek. I / Didaktik der Geometrie“. In Vorlesungsskripte von Jürgen Roth, Universität Koblenz-Landau.
- Präsentationsfolien zu Kapitel 5 „Problemlösen“ der Vorlesung „Didaktik der Mathematik in der Sek. I / Didaktik der Geometrie“. In Vorlesungsskripte von Jürgen Roth, Universität Koblenz-Landau.
Ergebnisse der Nachbereitung
Tragen Sie die Ergebnisse Ihrer Nachbereitung in die folgende Tabelle ein.
| Aufgabenstellung | Erwartungshorizont | Diskussion |
|---|---|---|
|
Die SuS stehen vor dieser Aufgabe:
Gibt es Dreiecke, welche die Bedingung
|
|
Zur Beantwortung der Aufgabe sind die erlernten Problemkategorien auf ein konkrete Fragstellung anzuwenden und die Phasen des Problemlösens an dem Problem zu näher erläutern. Zuletzt wird eine didaktische Analyse des Problems gefordert. |
Literaturhinweise
- „Erziehen im Mathematikunterricht.“ In: Kaenders & Schmidt (Hrsg.) Mit GeoGebra mehr Mathematik verstehen.
- Kapitel 3 „Konstruieren“ in Weigand et. al. (2018). „Didaktik der Geometrie für die Sekundarstufe I“
- Ladel & Kortenkamp (2016). „Artifact-Centric Activity Theory—A Framework for the Analysis of the Design and Use of Virtual Manipulatives“. In Moyer-Packenham (Hrsg.). International Perspectives on Teaching and Learning Mathematics with Virtual Manipulatives.
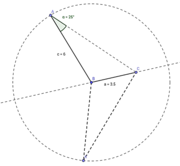
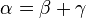 , erfüllen? Wenn ja welche? Begründe deine Antwort.
, erfüllen? Wenn ja welche? Begründe deine Antwort.
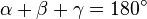
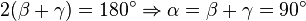
 und
und  noch eine weitere Bedingung/ Gleichung gestellt werden muss. Für den oben beschriebenen Lösungsweg wurde "nur" der Satz von der Winkelsumme im Dreieck und Äquivalenzumformungen gebraucht.
noch eine weitere Bedingung/ Gleichung gestellt werden muss. Für den oben beschriebenen Lösungsweg wurde "nur" der Satz von der Winkelsumme im Dreieck und Äquivalenzumformungen gebraucht.
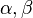 und
und 
