GeometrieUndUnterrichtSS2019 07: Unterschied zwischen den Versionen
(→Dokumentation der Sitzung) |
(→Ergebnisse der Nachbereitung) |
||
| (11 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 59: | Zeile 59: | ||
Erinnerung: Es geht um die Art & Weise wie Alice und Bob die die Aufgabenstellung bearbeitet haben.<br /> | Erinnerung: Es geht um die Art & Weise wie Alice und Bob die die Aufgabenstellung bearbeitet haben.<br /> | ||
| − | Zusammenfassend halten wir fest: Alice argumentiert mit intuitiven Begriffen, die nicht mathematischer Natur sind. Die Reihenfolge der Konstrukionsbeschreibung ist durcheinander und daher schwer zu folgen. Außerdem schreibt sie in der Ich-Form, während Bob eine Gebrauchsanweisung / Konstruktionsanweisung in neutraler Form schreibt. Es kam der Einwand, dass es in Geogebra nur schwer möglich ist, einen Winkel so zu verschieben, dass keine Nachkommastellen entstehen. Stattdessen hätte | + | Zusammenfassend halten wir fest: Alice argumentiert mit intuitiven Begriffen, die nicht mathematischer Natur sind. Die Reihenfolge der Konstrukionsbeschreibung ist durcheinander und daher schwer zu folgen. Außerdem schreibt sie in der Ich-Form, während Bob eine Gebrauchsanweisung / Konstruktionsanweisung in neutraler Form schreibt. Es kam der Einwand, dass es in Geogebra nur schwer möglich ist, einen Winkel so zu verschieben, dass keine Nachkommastellen entstehen. Stattdessen hätte Bob auch einfach einen festen Winkel konstruieren können.<br /> |
Wir halten '''zentrale Aspekte von Konstruktionsbeschreibungen''' an der Tafel fest:<br /> | Wir halten '''zentrale Aspekte von Konstruktionsbeschreibungen''' an der Tafel fest:<br /> | ||
| Zeile 69: | Zeile 69: | ||
* Erlaubte / Angemessene Operationen<br /> | * Erlaubte / Angemessene Operationen<br /> | ||
| − | + | -> Die Reihenfolge ist besonders für das Verständnis der anderen SuS und zur eigenen Überprüfung wichtig (vgl. Konstruktionsbeschreibung von Alice). Ob in der Ich-Perspektive oder aus neutraler Sichtweise geschrieben wird ist dabei variabel, es kommt dabei auf die Aufgabenstellung an; generell ist beides erlaubt. <br /> | |
Wir halten '''Ziele von Konstruktionsbeschreibungen''' an der Tafel fest:<br /> | Wir halten '''Ziele von Konstruktionsbeschreibungen''' an der Tafel fest:<br /> | ||
| Zeile 77: | Zeile 77: | ||
* Ermöglichung von Kommunikation über Konstruktionsaufgaben<br /> | * Ermöglichung von Kommunikation über Konstruktionsaufgaben<br /> | ||
| − | Außerdem muss die Klausursituation / Leistungsmessung beachtet werden: Lehrkräfte brauchen die Konstruktionsbeschreibungen um gelöste Aufgaben der SuS bewerten zu können. | + | -> Außerdem muss die Klausursituation / Leistungsmessung beachtet werden: Lehrkräfte brauchen die Konstruktionsbeschreibungen um gelöste Aufgaben der SuS bewerten zu können.<br /> |
| + | <br /> | ||
| + | |||
Es folgt ein kurzer Input zur '''„Artifact-Centric Activity Theory“''' (ACAT, Ladel & Kortenkamp, 2016) – siehe Literaturhinweise | Es folgt ein kurzer Input zur '''„Artifact-Centric Activity Theory“''' (ACAT, Ladel & Kortenkamp, 2016) – siehe Literaturhinweise | ||
| − | + | [[Datei:Artifact-Centric Activity Theory.PNG|thumb|Artifact-Centric Activity Theory]] | |
| − | + | Das Modell besteht aus folgenden Elementen: Subjekt (z.B. Schüler/in), Objekt (z.B. Mathematik) und Artefakt (z.B. Hilfsmittel wie Zirkel, Lineal, Papier). Das Artefakt vermittelt zwischen Subjekt und Objekt (beispielsweise hilft das Artefakt dem/der Schüler/in an das gegebene mathematische Problem heranzugehen). Der/Die Schüler/in gibt Arbeit in das Artefakt hinein, dabei entsteht ein Produkt und die Beobachtung von Handlungen ist sichtbar. Die Beziehung zwischen Artefakt und Objekt bzw. das Problem an sich kann jedoch beispielsweise nur durch die geforderte Konstruktionsbeschreibung sichtbar gemacht werden. Zirkel und Lineal erlauben diese Sichtbarkeit zum Beispiel nicht.<br /> | |
| − | + | Der Ursprung dieser Theorie geht auf den Umgang mit Stellenwerttafeln in der Grundschule zurück. Trotzdem passt dieser Ansatz gut zur Geometrie in der Sekundarstufe; besonders zum Thema Konstruieren. <br /> | |
| − | + | ||
| − | Das Modell besteht aus folgenden Elementen: Subjekt (z.B. Schüler/in), Objekt (z.B. Mathematik) und Artefakt (z.B. Hilfsmittel wie Zirkel, Lineal, Papier). Das Artefakt vermittelt zwischen Subjekt und Objekt (beispielsweise hilft das Artefakt dem/der Schüler/in an das gegebene mathematische Problem heranzugehen). Der/Die Schüler/in gibt Arbeit in das Artefakt hinein, dabei entsteht ein Produkt und die Beobachtung von Handlungen ist sichtbar. Die Beziehung zwischen Artefakt und Objekt bzw. das Problem an sich kann jedoch beispielsweise nur durch die geforderte Konstruktionsbeschreibung sichtbar gemacht werden. Zirkel und Lineal erlauben diese Sichtbarkeit zum Beispiel nicht. | + | |
| − | Der Ursprung dieser Theorie geht auf den Umgang mit Stellenwerttafeln in der Grundschule zurück. Trotzdem passt dieser Ansatz gut zur Geometrie in der Sekundarstufe; besonders zum Thema Konstruieren. | + | |
Anschließend an diese Theorie wird noch genannt, dass der Anspruch und der Umfang an eine Konstruktionsbeschreibung an der Lehrkraft selbst liegt. Es kann mit der Klasse individuell ausgemacht werden, welche Aspekte in einer Konstruktionsbeschreibung berücksichtigt werden müssen, dabei kommt es unter anderem auch auf die Klassenstufe an. | Anschließend an diese Theorie wird noch genannt, dass der Anspruch und der Umfang an eine Konstruktionsbeschreibung an der Lehrkraft selbst liegt. Es kann mit der Klasse individuell ausgemacht werden, welche Aspekte in einer Konstruktionsbeschreibung berücksichtigt werden müssen, dabei kommt es unter anderem auch auf die Klassenstufe an. | ||
:--> Sinn & Zweck von Konstruktionsbeschreibungen sollte nun erkannt sein! | :--> Sinn & Zweck von Konstruktionsbeschreibungen sollte nun erkannt sein! | ||
| Zeile 93: | Zeile 92: | ||
==== Input-Phase ==== | ==== Input-Phase ==== | ||
| − | Es folgt eine Diskussion/Austausch zu der Frage „Was ist ein Problem?“ (Folie 5). Verschiedene Meinungen zu den ersten drei Beispielen werden diskutiert | + | Es folgt eine Diskussion/Austausch zu der Frage „Was ist ein Problem?“ (Folie 5). Verschiedene Meinungen zu den ersten drei Beispielen werden diskutiert:<br /> |
| − | + | Muss man bei Beispiel 1 (Umfang eines Rechtecks mit Länge 32 m und Flächeninhalt 640m^2 berechnen) nur stumpf eine Formel anwenden oder auch den Zusammenhang zwischen Flächeninhalt und Umfang verstehen? Ist die Oberfläche und das Volumen eines Menschen zu bestimmen zu allgemein um ein Problem zu sein? Muss man dabei wissen wie schwer/groß der Mensch ist? Ist eine Aufgabe ein Problem wenn sie ganz allgemein, ohne Anforderungen und offen gestellt ist?<br /> | |
| + | Beispiel 2 (Oberfläche und Volumen eines Menschen bestimmen) ist ein '''Approximierungs- / Modellierungsproblem''', indem man den Körper des Menschen durch verschiedene Formen wie Kegel, Zylinder,… approximiert. Formuliert man Beispiel 3 (Form einer Verpackung für 3 Tennisbälle) so um, dass die Frage lautet: „Welche Größe sollte die Verpackung haben, dass das Oberfläche / Volumen maximal / minimal wird?“, so handelt es sich um ein '''Optimierungsproblem'''. (-> Weitere Klassifizierungen von Problemtypen, siehe Folie 8)<br /> | ||
| + | |||
| − | Auf Folie 6 folgt die Differenzierung eines Routine-Problems (Aufgabe) und einer Problemlöse-Aufgabe (Problem). Dabei kommt es darauf an, ob man den Algorithmus kennt oder nicht und die Klassifizierung hängt davon ab, wer sie lösen soll und ist daher subjektiv und Adressaten | + | Auf Folie 6 folgt die Differenzierung eines '''Routine-Problems (Aufgabe)''' und einer '''Problemlöse-Aufgabe (Problem)'''. Dabei kommt es darauf an, ob man den Algorithmus kennt oder nicht und die Klassifizierung hängt davon ab, wer sie lösen soll und ist daher subjektiv und vom Adressaten abhängig. Beispielsweise ist Beispiel 1 für uns oder auch höhere Klassenstufen keine Problemlöseaufgabe, aber für die Klasse 5 evtl. schon.<br /> |
| − | Die Definition von Problemlösen (Folie 7) lautet: „Ein Problemlöser kennt keine Lösung der Problemstellung, also weder einen Operator noch eine Operatorkette, die den Anfangszustand in den Zielzustand überführt.“ | + | Die Definition von Problemlösen (Folie 7) lautet: ''„Ein Problemlöser kennt keine Lösung der Problemstellung, also weder einen Operator noch eine Operatorkette, die den Anfangszustand in den Zielzustand überführt.“'' |
==== Arbeitsphase ==== | ==== Arbeitsphase ==== | ||
| Zeile 106: | Zeile 107: | ||
* Planentwickeln | * Planentwickeln | ||
* Rückschau | * Rückschau | ||
| − | Die Konstruktionsprobleme sollen mit Hilfe einer der folgenden | + | Die Konstruktionsprobleme sollen mit Hilfe einer der folgenden '''heuristischen Strategien''' (Folie 12) gelöst werden: |
* n-1 Methode (Weglassen einer Bedingung) | * n-1 Methode (Weglassen einer Bedingung) | ||
* Konstruktion von Teilkonfigurationen /-figuren | * Konstruktion von Teilkonfigurationen /-figuren | ||
| Zeile 116: | Zeile 117: | ||
'''Ergebnisse der Gruppenarbeit''' | '''Ergebnisse der Gruppenarbeit''' | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! !! Konstruktion 1!! Konstruktion 2!! Konstruktion 3!! Konstruktion 4 | ||
| + | |- | ||
| + | | Aufgabe|| Mittelpunkt des gegebenen Kreises konstruieren.|| Quadrat DEFG zum gegebenen spitzwinkligen Dreieck konstruieren.|| Dreieck zur gegebenen Seite a, Seitenhalbierenden s<sub>a</sub> und Höhe h<sub>c</sub> konstruieren.|| Kreis K konstruieren, so dass K die Kreisbögen und die beiden Halbkreise in je einem Punkt berührt und die Gesamtfigur achsensymmetrisch bleibt. | ||
| + | |- | ||
| + | | Typ|| || (n-1)-Methode|| Konstruktion einer Teilfigur|| Reduktion auf Berechnungsproblem | ||
| + | |- | ||
| + | | Bild|| || [[Datei:Konstruktion 2.PNG|thumb|(n-1)-Methode]]|| [[Datei:Konstruktion 3.PNG|thumb|Konstruktion einer Teilfigur]]|| [[Datei:Konstruktion 4.PNG|thumb|Reduktion auf Berechnungsproblem]] | ||
| + | |- | ||
| + | | Quelle || | ||
| + | || Folie 18 in den Präsentationsfolien zu Kapitel 5 „Problemlösen“ der Vorlesung „Didaktik der Mathematik in der Sek. I / Didaktik der Geometrie“. In Vorlesungsskripte von Jürgen Roth, Universität Koblenz-Landau. | ||
| + | || Folie 19 in den Präsentationsfolien zu Kapitel 5 „Problemlösen“ der Vorlesung „Didaktik der Mathematik in der Sek. I / Didaktik der Geometrie“. In Vorlesungsskripte von Jürgen Roth, Universität Koblenz-Landau. | ||
| + | || Folie 20 in den Präsentationsfolien zu Kapitel 5 „Problemlösen“ der Vorlesung „Didaktik der Mathematik in der Sek. I / Didaktik der Geometrie“. In Vorlesungsskripte von Jürgen Roth, Universität Koblenz-Landau. | ||
| + | |} | ||
== Nachbereitungsauftrag == | == Nachbereitungsauftrag == | ||
| − | Entwerfen Sie eine Prüfungsfrage bzw. ein kurzes Prüfungsgespräch zu den Sitzungen zum '' | + | Entwerfen Sie eine Prüfungsfrage bzw. ein kurzes Prüfungsgespräch zu den Sitzungen zum ''Konstrieren'' (I+II). Ihre Frage sollte dabei nicht nur bloße Wissensabfrage sein, sondern auch Anwendungen, Begründungen oder Diskussionen erfordern. (Sollte Ihnen doch nur Aufgaben zur bloßen Wissensabfrage einfallen, entwerfen Sie drei Prüfungsfragen.) |
# Formulieren Sie Ihre Prüfungsfrage bzw. den Anlass für das Prüfungsgespräch in der ''Aufgabenstellung''-Spalte. | # Formulieren Sie Ihre Prüfungsfrage bzw. den Anlass für das Prüfungsgespräch in der ''Aufgabenstellung''-Spalte. | ||
| Zeile 196: | Zeile 212: | ||
Die Aufgabe thematisiert die Unterscheidung Problem - Routineaufgabe und geht spezieller auf die Problemkategorien ein. Anschließend werden die Stratgien zur Problemlösung behandelt. | Die Aufgabe thematisiert die Unterscheidung Problem - Routineaufgabe und geht spezieller auf die Problemkategorien ein. Anschließend werden die Stratgien zur Problemlösung behandelt. | ||
<!-- === Abgabe Marc Ende | <!-- === Abgabe Marc Ende | ||
| + | <!-- === Abgabe Wibke Grundbrecher Anfang =========================================================================================================== --> | ||
| + | |- | ||
| + | | | ||
| + | Betrachte folgendes Problem:<br /> | ||
| + | Gegeben seien drei parallele Geraden a, b, c. Es soll ein gleichseitiges Dreieck ABC konstruiert werden, dessen Eckpunkte jeweils auf einer der drei gegebenen parallelen Geraden liegen.<br /> | ||
| + | * Welche der heuristischen Strategien kann angewandt werden, um ein solches Dreieck zu konstruieren? | ||
| + | * Wie kann man vorgehen, um dieses Problem zu Lösen? | ||
| + | || | ||
| + | Bei diesem Problem bietet sich die (n-1)-Methode, also das Weglassen einer Bedingung an.<br /> | ||
| + | Lege einen der Eckpunkte (O.E.) A auf die parallele Gerade a. Setze nun den Eckpunkt B beliebig auf b, um dann zu der Seite AB ein gleichseitiges Dreieck zu konstruieren. Daraus ergibt sich der Eckpunkt C, der vermutlich noch nicht auf c liegt. Verschiebe nun B auf b so, dass C auf c liegt. | ||
| + | [[Datei:Beispiel Parallele Geraden.jpg|thumb|(n-1)-Methode]] | ||
| + | |||
| + | || | ||
| + | Um diese Prüfungsfrage zu beantworten müssen die verschiedenen heuristischen Strategien bekannt sein. Zusätzlich wird durch ein konkretes Beispiel fachliches Geometrie-Wissen integriert. | ||
| + | <!-- === Abgabe Wibke Grundbrecher Ende ============================================================================================================ --> | ||
| + | <!-- === Abgabe Julian Anfang =========================================================================================================== --> | ||
| + | |- | ||
| + | | | ||
| + | Finden Sie die folgende Aufgabenstellung als Klausuraufgabe geeignet?<br /> | ||
| + | |||
| + | Ist die folgende Aussage wahr, oder falsch? Begründe! <br /> | ||
| + | |||
| + | Wenn zwei Geraden <math>g</math> und <math>h</math> parallel sind, dann bildet die Gerade <math>h</math> '''IMMER''' die Mittelparallele von den Geraden <math>g</math> und einer weiteren parallelen Geraden <math>i</math>, wenn die Gerade <math>i</math> doppelt so weit von <math>g</math> entfernt ist, wie von der Geraden <math>h</math>. | ||
| + | || | ||
| + | Um diese Aufgabenstellung zu beantworten, müssen die SuS die genaue Definition einer Mittelparallelen kennen.<br /> | ||
| + | |||
| + | ''Sind zwei parallele Geraden <math>g</math> und <math>h</math> gegeben, so ist ihre Mittelparallele die Gerade, die von <math>g</math> und <math>h</math> jeweils den gleichen Abstand hat.''<br /> | ||
| + | |||
| + | Hier gibt es aber auch gleich eine Schwierigkeit. Viele SuS werden wahrscheinlich argumentieren, dass wenn ich eine Gerade habe, die von zwei weiteren Geraden den gleichen Abstand hat, es sich um eine Mittelparallele handelt. Sie gehen davon aus, dass <math>h</math> die Mittelparallele ist und legen <math>i</math> auf die andere Seite wie <math>g</math>. Nachmessen zeigt, dass die Abstandsvoraussetzungen erfüllt sind. Die Aussage scheint also zu stimmen.<br /> | ||
| + | |||
| + | Dies ist jedoch nicht der Fall! In dieser Situation soll nämlich die Gerade <math>i</math> so konstruiert werden, dass <math>h</math> gerade NICHT die Mittelparallele ist. Wichtig in diesem Zusammenhang ist das Wort ''''''immer'''''' aus der Aufgabenstellung. Mit etwas überlegen, kann man nämlich leicht ein Gegenbeispiel konstruieren, wenn man die Gerade <math>i</math> zwischen die Geraden <math>g</math> und <math>h</math> legt. Dies muss nur von den SuS erkannt werden. <br /> | ||
| + | |||
| + | Die Aufgabe erscheint nicht sonderlich geeignet, da gerade das exakte Wissen über die Definition von Mittelparallele zum falschen Ergebnis führen kann. Genauso hat das finden des Gegenbeispiels sehr wahrscheinlich nichts, mit dem im Unterricht behandelten Wissen über Geometrie zu tun. Es wird hier nämlich, anders als es die Aufgabe vermuten lässt NICHTS so konstruiert, dass es sich bei der Geraden <math>h</math> um eine Mittelparallele handelt. | ||
| + | || | ||
| + | Um diese Prüfungsfrage beantworten zu können, muss sich der Prüfling über das Verständnis des Begriffs Mittelparallele für SuS im klaren sein und den Denkansatz der SuS beim Beginn einer Konstruktion nachvollziehen können. | ||
| + | <!-- === Abgabe Julian Ende ============================================================================================================ --> | ||
| + | <!-- === Abgabe Patrick Anfang =========================================================================================================== --> | ||
| + | |- | ||
| + | | | ||
| + | Folgende Aufgabe wird Schülern der Oberstufe gestellt:<br /> | ||
| + | Finde ein Verfahren zur Bestimmung des Abstands zwischen zwei windschiefen Geraden.<br /> | ||
| + | * In wie fern handelt es sich bei der gegebenen Aufgabe um ein Problem? | ||
| + | * Welche Lösungsstrategien können Schüler verfolgen? | ||
| + | * In wie weit unterscheidet sich die Aufgabe von dem Auftrag, den Abstand zweier Geraden gegeben einem geeigneten Verfahren auszurechnen? | ||
| + | || | ||
| + | * Ob es sich bei der gegebenen Aufgabe um ein Problem handelt, hängt vom Vorwissen der Schülerinnen und Schüler ab. Im Falle, dass sie die Formel bereits kennen, erübrigt sich das Problem. Andernfalls, können die Schülerinnen und Schüler die Aufgabe nur mit Hilfe einiger erfordelichen Grundvorstellungen lösen. Ein klassischer analytischer Weg führt über die Minimierung der Abstandsfunktion zweier allgemeiner Punkte auf den Geraden. In diesem Fall müsste jedoch bezüglich zwei Parametern optimiert werden. Dieser Weg kann in der Schule auf Grund des mangelnden Vorwissens nicht genutzt werden. Damit lässt sich die Aufgabe auch nicht als Routineproblem auffassen, das einem klassischen Optimierungsschema folgt. Vielmehr ist hier ein geometrischer Ansatz gefragt. Mit Hilfe geeigneter geometrischer Grundvorstellungen müssen die Schülerinnen und Schüler den Weg von den gegebenen Voraussetzungen zum Ziel selbst finden. Damit stellt die Aufgabe für sie ein Problem dar. | ||
| + | * Das Problem lässt sich geometrisch auf mindestens zwei Wegen lösen. Einer dieser Wege führt über das Vorwissen/die Heuristik, dass der Abstandsvektor senkrecht auf beiden Geraden stehen muss, sein Skalarprodukt mit den jeweiligen Richtungsvektoren also Null sein muss. Dadurch ergibt sich ein Gleichungssystem, dessen Lösung die gesuchten Parameter sind, welche angeben, welche Punkte durch den Abstandsvektor zu verbinden sind. Schließlich ist die Länge dieses Vektors der Abstand. Alternativ kann die Aufgabe mit Hilfe einer Hilfsebene gelöst werden. Legt man eine Ebene durch eine der Geraden, die Parallel zur zweiten Ebene ist, sind alle Punkte dieser zweiten Geraden gleich weit von der Hilfseben entfernt. Kennen die Schüler die Hesse'sche Normalform für Ebenen, so wissen sie auch, dass sich damit leicht der Abstand zwischen Ebene und einem Punkt ausrechnen lässt. Sie können also eine konkrete Formel angeben, welche den Abstand zwischen der Hilfsebene und einem beliebigen Punkt angibt. | ||
| + | * Diese Berechnungsaufgabe würde viel mehr einem Routine-Problem entsprechen, da die Schüler den erwarteten Lösungsweg bzw. einen "Problem-Löse-Algorithmus" für die Aufgabe kennen. Im Gegensatz dazu verlangt die vorherige Aufgabe neben geeignetem Vorwissen, einigen Transfer und Kreativität ab. Die Schüler kennen für die ursprüngliche Aufgabe keine fertige Methode vom Anfangs in den Zielzustand zu gelangen. | ||
| + | |||
| + | || | ||
| + | * Charakterisierung eines Problems wird diskutiert | ||
| + | * Mögliche Lösungsstrategien werden erörtert | ||
| + | * Unterschiede zwischen Problem und Routine-Problem werden herausgearbeitet | ||
| + | |||
| + | <!-- === Abgabe Patrick Ende ============================================================================================================ --> | ||
<!-- === Tabelle Ende ====================================================================================================================== --> | <!-- === Tabelle Ende ====================================================================================================================== --> | ||
|} | |} | ||
Aktuelle Version vom 21. Juni 2019, 09:05 Uhr
Inhaltsverzeichnis |
Vorbereitungsauftrag
Die Schüler*in Alice und Bob haben die unten stehende Aufgabe bearbeitet.
- Bewerten Sie zunächst die jeweiligen Konstruktionsbeschreibungen der Schüler*innen. Diskutieren Sie gegebenenfalls Fehler.
- Führen Sie die Konstruktion gemäß der Konstruktionsbeschreibungen durch. Diskutieren Sie gegebenenfalls Probleme, die Ihnen bei der Durchführung auffallen.
Dreieckskonstruktion SSWk
Konstruiere ein Dreieck ABC mit den folgenden Eigenschaften: 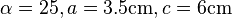 . Beschreibe deine Konstruktion.
. Beschreibe deine Konstruktion.
Konstruktionsbeschreibung von Alice (Zirkel & Lineal)
- Ich ziehe einen 6cm langen Strich. Am rechten Ende (B) steche ich den Zirkel in das Blatt und stelle ihn auf 3,5 cm ein. Jetzt zirkle ich einen Halbkreis nach oben. Dieser Halbkreis schneidet den Winkel, den ich vorher am linken Ende der Strecke mit dem Geodreieck eingezeichnet habe, in zwei Punkten. Jetzt verbinde ich die erhaltenen Punkte miteinander und sehe, dass es zwei Dreiecke gibt, die die SSWk=Konnsstruktion erfüllen.
Quelle: „Erziehen im Mathematikunterricht.“ In: Kaenders & Schmidt (Hrsg.) Mit GeoGebra mehr Mathematik verstehen.
Konstruktionsbeschreibung von Bob (GeoGebra)
- Zeichne Strecke a mit Länge 3,5cm. Zeichne Kreis um B mit Länge 6cm. Erstelle Punkt A auf dem Kreis und Messe den Winkel α = ∠BAC. Verschiebe Punkt A auf dem Kreis so, dass α = 25°. Spiegele das Dreieck ABC an a. Ich habe jetzt zwei Dreiecke, die die Bedingungen erfüllen.
Ergebnisse des Vorbereitungsauftrags
Bearbeitung von Ilona
Die Konstruktionsbeschreibung von Alice verwendet tendentiell einfachere Begriffe und vermeidet konkrete mathematische Bezeichnungen (z.B. Strich statt Strecke von A nach B). Auch folgt sie in der Beschreibung der Schritte nicht der tatsächlichen Reihenfolge, sondern springt zwischendurch zurück ("Winkel, den ich vorher...eingezeichnet habe"). Darüber hinaus bezeichnet Alice die geometrischen Objekte ihrer Konstruktion nicht eindeutig (z.B. "am linken Ende der Strecke"). Allerdings konstruiert sie zwei Dreiecke, welche die Anforderungen erfüllen, wenn auch die Formulierung "Jetzt verbinde ich die erhaltenen Punkte" wieder nicht sehr präzise ist und nur erahnen lässt, was genau dieser Schritt beinhaltet. Bob hingegen formuliert meiner Meinung nach präziser und unter Verwendung mathematischer Begriffe sein Vorgehen. Beispielsweise führt er die Benennung der Punkte, Winkel und Strecken seiner Konstruktion stringent durch. Bob hat seine Konstruktion offenbar mit Hilfe von Geogebra durchgeführt, wodurch es ihm möglich war, den Punkt A auf dem Kreis um B zu verschieben, bis der Winkel α die gewollte Größe hatte. Konstruiert man mit Zirkel und Lineal, so erweist sich dieses Vorgehen jedoch als schwierig und der Ansatz von Alice als praktikabler. Auch hat Bob durch seine Spiegelung an der durch a verlaufenden Gerade lediglich zwei Dreiecke konstruiert, die zueinander kongruent bzw. durch Verschiebung / Spiegelung / Drehung ineinander überführbar sind. Das Dreieck, welches Alice zusätzlich gefunden hat, fehlt in Bobs Konstruktion (es wurde aber auch nur die Konstruktion eines Dreiecks in der Aufgabenstellung gefordert). Die Konstruktionsbeschreibung von Alice lässt sich recht gut durchführen, wenn man die fehlenden Benennungen der geometrischen Objekte für sich erschließt. Bobs Beschreibung funktioniert gut bis zu dem Punkt, an welchem er den Punkt A auf dem Kreis verschiebt, bis der Winkel stimmt. Dieser Schritt lässt sich nur mit Hilfsmitteln wie Geogebra leicht durchführen.
Bearbeitung von Wibke
Alice’s Konstruktionsbeschreibung führt zum Ziel, jedoch ist ihre Ausdrucksweise nicht fachlich korrekt. Sie sollte folgende sprachlichen Formulierungen beachten:
Strich – Strecke von A nach B
In das Blatt – Zirkel bei B ansetzen
Zirkle Halbkreis nach oben – Zeichne Kreis um B
Schneidet Winkel – schneidet die Gerade
Linkes Ende – Punkt A
Punkte verbinden – Stecken AC, AC‘
Außerdem, sollte die Konstruktionsbeschreibung in der Reihenfolge geschrieben werden, in welcher auch die einzelnen Schritte durchgeführt werden.
Bob’s Konstruktionsbeschreibung führt ebenfalls zum Ziel. Er konstruiert mit Hilfe von Geogebra zwei kongruente Dreiecke. Falls die Aufgabenstellung nur so gegeben wird, ohne konkrete Hilfsmittel zu nennen, halte ich seine Ausführung für gut. Will man, dass die SuS mit Zirkel und Lineal arbeiten, sollte dies explizit in der Aufgabenstellung genannt werden.
Bearbeitung von Anna-Lena
Meine Vorredner haben die wichtigsten Bemerkungen zu den beiden Konstruktionsbeschreibungen schon gemacht. Diesen stimme ich zu, weshalb ich hier nur noch ergänze: Aus der Konstruktionsbeschreibung von Alice geht die Konstruktion eines zweiten Dreiecks nicht hervor, da sie nur einen Winkel in B abträgt und von einem Zweiten, nach unten Gespiegelten nie die Rede war. Die Konstruktionsbeschreibung ist deshalb meiner Meinung nach auch bei Hinwegsehen der (fach-)sprachlichen Mängel und der Reihenfolge nicht vollkommen richtig. Dennoch nennt sie die entscheidenden Konstruktionsschritte. Die Konstruktionsbschreibung zeigt auch wie wichtig das Training und auch die häufige Kontrolle der logischen Argumentationsweise sowie der korrekte Fachsprache bei den Texten der SuS ist.
Bob's Konstruktionsbeschreiben lässt sich ohne Probleme nachvollziehen. Sein Ansatz ist in dem Sinne interessant, dass sich durch die Variation der Winkelbreite eine dynamische Konstruktion entwickelt. Er kann durch den Prozess entdecken, dass die Angaben SSW bis auf Konkruenz ein solches Dreieck eindeutig bestimmen und wie sich das Dreieck beim Abändern einer Größe verändert. Darauf müssen SuS meiner Meinung bei Konstruktionen mit Zirkel und Lineal eher aufmerksam gemacht werden. Die Konstruktion des Dreieck mit Bob's Methode bedarf jedoch höchst wahrscheinlich mehrerer Schritte, s.d. das das Hilfmittel Geogebra bis auf den obenen genannten keinen Vorteil bringt.
Bei beiden Ansätzen stellt sich mir die Frage, ob die Konstruktion des zweiten Dreiecks die Aufgabe überhaupt erfüllt. Da "ein(?)" Dreieck ABC konstruiert werden sollte und nicht das Dreieck ACB.
Sitzungsmaterialien
- Begleitfolien der Sitzung vom 07.06.2019
- Arbeitsblätter zu Konstruktionsaufgaben und idealtypische Problemlöseprozesse
Dokumentation der Sitzung
Ergebnisse der Vorbereitungsaufträge
Erinnerung: Es geht um die Art & Weise wie Alice und Bob die die Aufgabenstellung bearbeitet haben.
Zusammenfassend halten wir fest: Alice argumentiert mit intuitiven Begriffen, die nicht mathematischer Natur sind. Die Reihenfolge der Konstrukionsbeschreibung ist durcheinander und daher schwer zu folgen. Außerdem schreibt sie in der Ich-Form, während Bob eine Gebrauchsanweisung / Konstruktionsanweisung in neutraler Form schreibt. Es kam der Einwand, dass es in Geogebra nur schwer möglich ist, einen Winkel so zu verschieben, dass keine Nachkommastellen entstehen. Stattdessen hätte Bob auch einfach einen festen Winkel konstruieren können.
Wir halten zentrale Aspekte von Konstruktionsbeschreibungen an der Tafel fest:
- Grad der mathematischen Fachsprache
- Reihenfolge der Operationen
- Unterscheidung von Objekten / Begriffen
- Anweisung vs. Erzählung
- Erlaubte / Angemessene Operationen
-> Die Reihenfolge ist besonders für das Verständnis der anderen SuS und zur eigenen Überprüfung wichtig (vgl. Konstruktionsbeschreibung von Alice). Ob in der Ich-Perspektive oder aus neutraler Sichtweise geschrieben wird ist dabei variabel, es kommt dabei auf die Aufgabenstellung an; generell ist beides erlaubt.
Wir halten Ziele von Konstruktionsbeschreibungen an der Tafel fest:
- Erziehung zu sprachlicher Genauigkeit
- Nachvollziehbare Dokumentation des eigenen Vorgehens; Wichtig für Nachbereitung / Modulanwendung
- Ermöglichung von Kommunikation über Konstruktionsaufgaben
-> Außerdem muss die Klausursituation / Leistungsmessung beachtet werden: Lehrkräfte brauchen die Konstruktionsbeschreibungen um gelöste Aufgaben der SuS bewerten zu können.
Es folgt ein kurzer Input zur „Artifact-Centric Activity Theory“ (ACAT, Ladel & Kortenkamp, 2016) – siehe Literaturhinweise
Das Modell besteht aus folgenden Elementen: Subjekt (z.B. Schüler/in), Objekt (z.B. Mathematik) und Artefakt (z.B. Hilfsmittel wie Zirkel, Lineal, Papier). Das Artefakt vermittelt zwischen Subjekt und Objekt (beispielsweise hilft das Artefakt dem/der Schüler/in an das gegebene mathematische Problem heranzugehen). Der/Die Schüler/in gibt Arbeit in das Artefakt hinein, dabei entsteht ein Produkt und die Beobachtung von Handlungen ist sichtbar. Die Beziehung zwischen Artefakt und Objekt bzw. das Problem an sich kann jedoch beispielsweise nur durch die geforderte Konstruktionsbeschreibung sichtbar gemacht werden. Zirkel und Lineal erlauben diese Sichtbarkeit zum Beispiel nicht.
Der Ursprung dieser Theorie geht auf den Umgang mit Stellenwerttafeln in der Grundschule zurück. Trotzdem passt dieser Ansatz gut zur Geometrie in der Sekundarstufe; besonders zum Thema Konstruieren.
Anschließend an diese Theorie wird noch genannt, dass der Anspruch und der Umfang an eine Konstruktionsbeschreibung an der Lehrkraft selbst liegt. Es kann mit der Klasse individuell ausgemacht werden, welche Aspekte in einer Konstruktionsbeschreibung berücksichtigt werden müssen, dabei kommt es unter anderem auch auf die Klassenstufe an.
- --> Sinn & Zweck von Konstruktionsbeschreibungen sollte nun erkannt sein!
Komplexere Konstruktionsaufgaben in der Perspektive des Problemlösens
Input-Phase
Es folgt eine Diskussion/Austausch zu der Frage „Was ist ein Problem?“ (Folie 5). Verschiedene Meinungen zu den ersten drei Beispielen werden diskutiert:
Muss man bei Beispiel 1 (Umfang eines Rechtecks mit Länge 32 m und Flächeninhalt 640m^2 berechnen) nur stumpf eine Formel anwenden oder auch den Zusammenhang zwischen Flächeninhalt und Umfang verstehen? Ist die Oberfläche und das Volumen eines Menschen zu bestimmen zu allgemein um ein Problem zu sein? Muss man dabei wissen wie schwer/groß der Mensch ist? Ist eine Aufgabe ein Problem wenn sie ganz allgemein, ohne Anforderungen und offen gestellt ist?
Beispiel 2 (Oberfläche und Volumen eines Menschen bestimmen) ist ein Approximierungs- / Modellierungsproblem, indem man den Körper des Menschen durch verschiedene Formen wie Kegel, Zylinder,… approximiert. Formuliert man Beispiel 3 (Form einer Verpackung für 3 Tennisbälle) so um, dass die Frage lautet: „Welche Größe sollte die Verpackung haben, dass das Oberfläche / Volumen maximal / minimal wird?“, so handelt es sich um ein Optimierungsproblem. (-> Weitere Klassifizierungen von Problemtypen, siehe Folie 8)
Auf Folie 6 folgt die Differenzierung eines Routine-Problems (Aufgabe) und einer Problemlöse-Aufgabe (Problem). Dabei kommt es darauf an, ob man den Algorithmus kennt oder nicht und die Klassifizierung hängt davon ab, wer sie lösen soll und ist daher subjektiv und vom Adressaten abhängig. Beispielsweise ist Beispiel 1 für uns oder auch höhere Klassenstufen keine Problemlöseaufgabe, aber für die Klasse 5 evtl. schon.
Die Definition von Problemlösen (Folie 7) lautet: „Ein Problemlöser kennt keine Lösung der Problemstellung, also weder einen Operator noch eine Operatorkette, die den Anfangszustand in den Zielzustand überführt.“
Arbeitsphase
Die Erarbeitung des Arbeitsauftrags erfolgt in 4 Gruppen, welche jeweils verschiedene Konstruktionsprobleme lösen sollen. Dabei soll das eigene Vorgehen anhand eines Leitfadens dokumentiert werden (Arbeitsblätter siehe unter "Sitzungsmaterialien").
Die Konstruktionsschritte werden dabei mit Hilfe eines Phasenmodells festgehalten. Dieses Modell beinhaltet folgende drei Aspekte:
- Problemverstehen
- Planentwickeln
- Rückschau
Die Konstruktionsprobleme sollen mit Hilfe einer der folgenden heuristischen Strategien (Folie 12) gelöst werden:
- n-1 Methode (Weglassen einer Bedingung)
- Konstruktion von Teilkonfigurationen /-figuren
- Reduktion auf Berechnungsproblem
Dabei können die heuristischen Strategien folgender Maßen kategorisiert werden (Folie 11):
- Inhaltliches / konkret-experimentelles Lösen (z.B. Grundschule)
- Nutzung von Darstellungen und Darstellungswechsel
- Vorwärts-/Rückwärtsarbeiten (z.B. Übungszettel im Mathestudium)
Ergebnisse der Gruppenarbeit
| Konstruktion 1 | Konstruktion 2 | Konstruktion 3 | Konstruktion 4 | |
|---|---|---|---|---|
| Aufgabe | Mittelpunkt des gegebenen Kreises konstruieren. | Quadrat DEFG zum gegebenen spitzwinkligen Dreieck konstruieren. | Dreieck zur gegebenen Seite a, Seitenhalbierenden sa und Höhe hc konstruieren. | Kreis K konstruieren, so dass K die Kreisbögen und die beiden Halbkreise in je einem Punkt berührt und die Gesamtfigur achsensymmetrisch bleibt. |
| Typ | (n-1)-Methode | Konstruktion einer Teilfigur | Reduktion auf Berechnungsproblem | |
| Bild | ||||
| Quelle | Folie 18 in den Präsentationsfolien zu Kapitel 5 „Problemlösen“ der Vorlesung „Didaktik der Mathematik in der Sek. I / Didaktik der Geometrie“. In Vorlesungsskripte von Jürgen Roth, Universität Koblenz-Landau. | Folie 19 in den Präsentationsfolien zu Kapitel 5 „Problemlösen“ der Vorlesung „Didaktik der Mathematik in der Sek. I / Didaktik der Geometrie“. In Vorlesungsskripte von Jürgen Roth, Universität Koblenz-Landau. | Folie 20 in den Präsentationsfolien zu Kapitel 5 „Problemlösen“ der Vorlesung „Didaktik der Mathematik in der Sek. I / Didaktik der Geometrie“. In Vorlesungsskripte von Jürgen Roth, Universität Koblenz-Landau. |
Nachbereitungsauftrag
Entwerfen Sie eine Prüfungsfrage bzw. ein kurzes Prüfungsgespräch zu den Sitzungen zum Konstrieren (I+II). Ihre Frage sollte dabei nicht nur bloße Wissensabfrage sein, sondern auch Anwendungen, Begründungen oder Diskussionen erfordern. (Sollte Ihnen doch nur Aufgaben zur bloßen Wissensabfrage einfallen, entwerfen Sie drei Prüfungsfragen.)
- Formulieren Sie Ihre Prüfungsfrage bzw. den Anlass für das Prüfungsgespräch in der Aufgabenstellung-Spalte.
- Beschreiben Sie ausführlich, wie mögliche (richtige) Antworten auf Ihre Frage aussehen könnten bzw. welche Aspekte in einem Prüfungsgespräch zu dieser Frage angesprochen werden sollten. Tragen Sie dies entsprechend in die Erwartungshorizont-Spalte ein.
- Erläutern Sie kurz, warum Sie diese Aufgabe einen zentralen Aspekt der Sitzung abdeckt und welche Anforderung an Wissen/Kompetenzen die Aufgabe fordert.
Unter den übergreifenden Literaturhinweise sind insbesondere relevant:
- „Erziehen im Mathematikunterricht.“ In: Kaenders & Schmidt (Hrsg.) Mit GeoGebra mehr Mathematik verstehen.
- Kapitel 3 „Konstruieren“ in Weigand et. al. (2018). „Didaktik der Geometrie für die Sekundarstufe I“
- Präsentationsfolien zu Kapitel 3 „Konstruieren“ der Vorlesung „Didaktik der Mathematik in der Sek. I / Didaktik der Geometrie“. In Vorlesungsskripte von Jürgen Roth, Universität Koblenz-Landau.
- Präsentationsfolien zu Kapitel 5 „Problemlösen“ der Vorlesung „Didaktik der Mathematik in der Sek. I / Didaktik der Geometrie“. In Vorlesungsskripte von Jürgen Roth, Universität Koblenz-Landau.
Ergebnisse der Nachbereitung
Tragen Sie die Ergebnisse Ihrer Nachbereitung in die folgende Tabelle ein.
| Aufgabenstellung | Erwartungshorizont | Diskussion |
|---|---|---|
|
Die SuS stehen vor dieser Aufgabe:
Gibt es Dreiecke, welche die Bedingung
|
|
Zur Beantwortung der Aufgabe sind die erlernten Problemkategorien auf ein konkrete Fragstellung anzuwenden und die Phasen des Problemlösens an dem Problem zu näher erläutern. Zuletzt wird eine didaktische Analyse des Problems gefordert. |
|
Betrachten Sie die folgende Aufgabe für SuS der achten Klasse: Bestimme das Volumen des geometrischen Objekts, welches die orangene Grundfläche hat und eine Höhe von 5 cm aufweist.
|
|
Die Aufgabe greift die unterschiedlichen Arten von Problemen im Kontext des Geometrieunterrichts auf und vertieft durch die Anwendung an einem konkreten Beispiel. Auch die theoretischen Grundlagen zu Grundbegriffen und -Konzepten der Geometrie werden angesprochen und mann muss sich damit auseinandersetzen, auf welchem Stand die SuS in der 8. Klasse sind, bzw. welche Schwierigkeiten eine solche Aufgabe mit sich bringt. |
|
Betrachtet wird folgende Situation: (In der Unterstufe) Bei 𝑛 Geraden (𝑛> 1) kann es maximal 𝑘 = 1 + 2 +⋯+ (𝑛−1) Schnittpunkte geben.
|
|
Die Aufgabe thematisiert die Unterscheidung Problem - Routineaufgabe und geht spezieller auf die Problemkategorien ein. Anschließend werden die Stratgien zur Problemlösung behandelt. |
|
Betrachte folgendes Problem:
|
Bei diesem Problem bietet sich die (n-1)-Methode, also das Weglassen einer Bedingung an. |
Um diese Prüfungsfrage zu beantworten müssen die verschiedenen heuristischen Strategien bekannt sein. Zusätzlich wird durch ein konkretes Beispiel fachliches Geometrie-Wissen integriert. |
|
Finden Sie die folgende Aufgabenstellung als Klausuraufgabe geeignet? Ist die folgende Aussage wahr, oder falsch? Begründe! Wenn zwei Geraden |
Um diese Aufgabenstellung zu beantworten, müssen die SuS die genaue Definition einer Mittelparallelen kennen. Sind zwei parallele Geraden Hier gibt es aber auch gleich eine Schwierigkeit. Viele SuS werden wahrscheinlich argumentieren, dass wenn ich eine Gerade habe, die von zwei weiteren Geraden den gleichen Abstand hat, es sich um eine Mittelparallele handelt. Sie gehen davon aus, dass Dies ist jedoch nicht der Fall! In dieser Situation soll nämlich die Gerade Die Aufgabe erscheint nicht sonderlich geeignet, da gerade das exakte Wissen über die Definition von Mittelparallele zum falschen Ergebnis führen kann. Genauso hat das finden des Gegenbeispiels sehr wahrscheinlich nichts, mit dem im Unterricht behandelten Wissen über Geometrie zu tun. Es wird hier nämlich, anders als es die Aufgabe vermuten lässt NICHTS so konstruiert, dass es sich bei der Geraden |
Um diese Prüfungsfrage beantworten zu können, muss sich der Prüfling über das Verständnis des Begriffs Mittelparallele für SuS im klaren sein und den Denkansatz der SuS beim Beginn einer Konstruktion nachvollziehen können. |
|
Folgende Aufgabe wird Schülern der Oberstufe gestellt:
|
|
|
Literaturhinweise
- „Erziehen im Mathematikunterricht.“ In: Kaenders & Schmidt (Hrsg.) Mit GeoGebra mehr Mathematik verstehen.
- Kapitel 3 „Konstruieren“ in Weigand et. al. (2018). „Didaktik der Geometrie für die Sekundarstufe I“
- Ladel & Kortenkamp (2016). „Artifact-Centric Activity Theory—A Framework for the Analysis of the Design and Use of Virtual Manipulatives“. In Moyer-Packenham (Hrsg.). International Perspectives on Teaching and Learning Mathematics with Virtual Manipulatives.
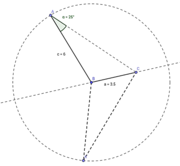



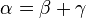 , erfüllen? Wenn ja welche? Begründe deine Antwort.
, erfüllen? Wenn ja welche? Begründe deine Antwort.
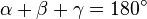
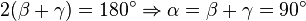
 und
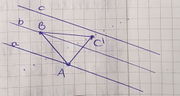
und  noch eine weitere Bedingung/ Gleichung gestellt werden muss. Für den oben beschriebenen Lösungsweg wurde "nur" der Satz von der Winkelsumme im Dreieck und Äquivalenzumformungen gebraucht.
noch eine weitere Bedingung/ Gleichung gestellt werden muss. Für den oben beschriebenen Lösungsweg wurde "nur" der Satz von der Winkelsumme im Dreieck und Äquivalenzumformungen gebraucht.
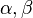 und
und 
 und
und  parallel sind, dann bildet die Gerade
parallel sind, dann bildet die Gerade 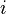 , wenn die Gerade
, wenn die Gerade 
