Wurzel aus 2 ist irrational: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Satz: Die Wurzel aus 2 ist irrational) |
(→Satz: Die Wurzel aus 2 ist irrational) |
||
| Zeile 2: | Zeile 2: | ||
Annahme: <math>\sqrt{2}</math> ist rational.<br /> | Annahme: <math>\sqrt{2}</math> ist rational.<br /> | ||
d.h. <math>\sqrt{2}=\frac{p}{q}, p,q \in \mathbb{N}</math>. | d.h. <math>\sqrt{2}=\frac{p}{q}, p,q \in \mathbb{N}</math>. | ||
| + | |||
| + | Beweis durch Widerspruch. <br /> | ||
| + | Annahme: <math>\sqrt{2}</math> = rational | ||
| + | |||
| + | D.h. <math>\exists</math> p,q <math>\in</math> <math>\mathbb{N}</math> : <math>\frac{p}{q}</math> = <math>\sqrt{2}</math> , mit p,q sind teilerfremd. <br /> | ||
| + | |||
| + | <math>\Rightarrow</math> <math>\frac{p^2}{q^2}</math> = 2 <br /> | ||
| + | <math>\Rightarrow</math> <math>p^2</math> = <math>2q^2</math> <br /> | ||
| + | <math>p^2</math> ist gerade. <math>\Rightarrow</math> p=2n, mit n <math>\in</math> <math>\mathbb{N}</math> <br /> | ||
| + | <math>\Rightarrow</math> <math>(2n)^2</math> = <math>2q^2</math> <br /> | ||
| + | <math>\Rightarrow</math> <math>4n^2</math> = <math>2q^2</math> <br /> | ||
| + | <math>\Rightarrow</math> <math>2n^2</math> = <math>q^2</math> <br /> | ||
| + | <math>\Rightarrow</math> q ist ebenfalls gerade <math>\Rightarrow</math> p und q sind nicht teilerfremd. <br /> | ||
| + | <math>\Rightarrow</math> <math>\frac{p^2}{q^2}</math> ist kürzbar. <br /> | ||
| + | <math>\Rightarrow</math> <math>\sqrt{2}</math> = irrational <br /> | ||
Aktuelle Version vom 31. Oktober 2019, 08:48 Uhr
Satz: Die Wurzel aus 2 ist irrational
Annahme: 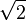 ist rational.
ist rational.
d.h. 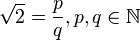 .
.
Beweis durch Widerspruch.
Annahme: 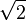 = rational
= rational
D.h.  p,q
p,q 
 :
: 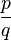 =
= 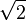 , mit p,q sind teilerfremd.
, mit p,q sind teilerfremd.

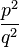 = 2
= 2

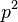 =
= 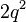
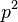 ist gerade.
ist gerade.  p=2n, mit n
p=2n, mit n 


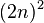 =
= 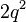

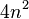 =
= 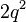

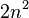 =
= 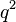
 q ist ebenfalls gerade
q ist ebenfalls gerade  p und q sind nicht teilerfremd.
p und q sind nicht teilerfremd.

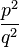 ist kürzbar.
ist kürzbar.

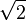 = irrational
= irrational

