Lösung von Aufgabe 12.1: Unterschied zwischen den Versionen
(→Frage) |
|||
| (21 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 24: | Zeile 24: | ||
== Lösung 1 == | == Lösung 1 == | ||
| − | Ja, der Fall, dass <math>P \in CB</math> muss durchdacht werden, da die Lage des Punktes <u>theoretisch</u> überall im Schnittpunkt der Halbebenen ligen kann. Wenn man den zweiten Teil des Beweises (ohne Hilfskonstruktion) betrachtet, ist die (mögliche) Lage von <math>P</math> nicht sofort ersichtlich. | + | Ja, der Fall, dass <math>P \in CB</math> muss durchdacht werden, da die Lage des Punktes <u>theoretisch</u> überall im Schnittpunkt der Halbebenen ligen kann. Wenn man den zweiten Teil des Beweises (ohne Hilfskonstruktion) betrachtet, ist die (mögliche) Lage von <math>\ P</math> nicht sofort ersichtlich. |
| − | <br />Allerdings kann man auch begründen: Nein, man muss den Fall nicht aufführen, da es trivial ist, die Lage von <math>P auf CB</math> zu widerlegen. Man kann es sich bildlich so vorstellen, dass <math>P</math> mithilfe des Mittelpunktes der Strecke <math>\overline {AB}</math> konstruiert wurde und deshalb - sollte <math>P \in CB</math> sein - die Strahlen <math>CA^+ CM^+ und CB^+ | + | <br />Allerdings kann man auch begründen: Nein, man muss den Fall nicht aufführen, da es trivial ist, die Lage von <math>\ P \ auf \ CB</math> zu widerlegen. Man kann es sich bildlich so vorstellen, dass <math>\ P</math> ja mithilfe des Mittelpunktes der Strecke <math>\overline {AB}</math> konstruiert wurde und deshalb - sollte <math>P \in CB</math> sein - die Strahlen <math>\ CA^+ \ CM^+ \ und \ CB^+</math> identisch seien. |
| + | --[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 21:16, 11. Jul. 2010 (UTC) | ||
| + | |||
| + | |||
| + | == Lösung 2 == | ||
| + | Wenn wir mit einem indirekten Beweis zeigen dass P nicht in der Halbebene <math>\ CB,A^-</math> <br /> liegen kann (haben wir), so gilt das für die komplette GESCHLOSSENE Halbebene <math>\ CB,A^-</math> <br /> d.h. auch für die Trägergerade CB. | ||
| + | Wir wissen also schon dass P nicht auf CB liegen kann, dieser Teil ist also überflüssig... | ||
| + | --[[Benutzer:Principella|Principella]] 19:59, 19. Jul. 2010 (UTC) | ||
| + | |||
| + | |||
| + | == Frage == | ||
| + | Unabhängig von der Aufgabenstellung mal: Müsste ich falls ich das zeigen müsste nich auch genau so zeigen, dass | ||
| + | P nicht auf der Geraden AB liegen kann? --[[Benutzer:TheGeosi|TheGeosi]] 08:24, 21. Jul. 2010 (UTC) | ||
| + | |||
| + | In diesem Fall definitiv nicht, aber es kommt immer drauf an wie wir den Beweis geführt haben. Wenn es ein indirekter Beweis ist, nehmen wir genau das an, was wir nicht wollen und schließen beim Widerspruch alles "Angenommene" automatisch aus. | ||
| + | 1) ist zwar ein direkter Beweis, aber es ist dasselbe Prinzip. Wir sagen dass P NICHT in ein und derselben (geschlossenen) Halbebene mit C liegen kann (Begründung = Konstruktion von P), also bleibt nur noch eine Möglichkeit = P liegt in der OFFENEN Halbebene AB,C- (d.h. ohne AB) | ||
| + | --[[Benutzer:Principella|Principella]] 11:28, 21. Jul. 2010 (UTC) | ||
| + | |||
| + | Ich denke auch, dass wir das nicht beweisen müssen, da wir nach Konstruktion P und C in verschiedene Halbebenen bezüglich AB gesteckt haben. Die Frage, ob P auf CB liegt geht ja ein wenig in die selbe Richtung, kann also von der Konstruktion abgeleitet werden. In dem Fall (Frage, ob P auf AB liegen kann) ist es jedoch sofort einsichtig! | ||
| + | --[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 12:36, 21. Jul. 2010 (UTC) | ||
Aktuelle Version vom 21. Juli 2010, 13:36 Uhr
Inhaltsverzeichnis |
Der schwache Außenwinkelsatz
Aufgabenstellung
Überprüfen Sie Ihr Verständnis: Ist Schritt 2.a im Beweis des schwachen Außenwinkelsatzes wirklich nötig? Wenn ja warum?
Der schwache Außenwinkelsatz
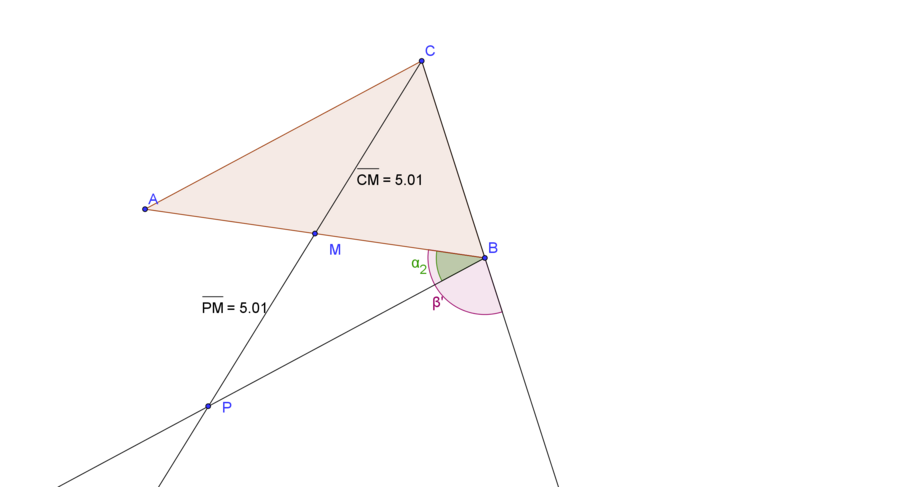
Hier nochmal: der Beweisschritt 2a, die Bezeichnungen wurden angepasst, bzw. stimmen mit der Skizze nun überein.
Das offene Innere von 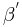 ist der Schnitt zweier offener Halbebenen
ist der Schnitt zweier offener Halbebenen  .
.
Der Punkt  würde gerade dann nicht im Inneren des Winkels
würde gerade dann nicht im Inneren des Winkels 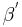 liegen,wenn er
liegen,wenn er
- in Halbenbene
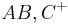
oder
- in der Halbebene
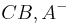
liegen würde.
zu 1.
Als Punkt der Halberaden 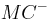 (Konstruktion von
(Konstruktion von  ) kann
) kann  nicht mit
nicht mit  auf ein und derselben Seite bezüglich
auf ein und derselben Seite bezüglich  liegen.
liegen.
zu 2.
2.a
Annahme: 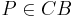 In diesem Fall würde gelten:
In diesem Fall würde gelten: 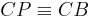 . (Begründung mittels Inzidenzaxiomen ist jetzt nicht mehr nötig.) Wir wollen uns darauf einigen die Gerade
. (Begründung mittels Inzidenzaxiomen ist jetzt nicht mehr nötig.) Wir wollen uns darauf einigen die Gerade  mit
mit  zu bezeichnen.
zu bezeichnen.
Die Gerade 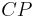 hat mit der Geraden
hat mit der Geraden  genau einen Punkt gemeinsam, den Punkt
genau einen Punkt gemeinsam, den Punkt  .
.
Die Gerade 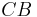 hat mit der Geraden
hat mit der Geraden  genau einen Punkt gemeinsam, den Punkt
genau einen Punkt gemeinsam, den Punkt  .
.
Da die beiden Geraden 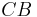 und
und 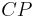 identisch sind und die nichtidentischen Geraden
identisch sind und die nichtidentischen Geraden  und
und  maximal einen Punkt gemeinsam haben können,
maximal einen Punkt gemeinsam haben können,
müssen die beiden Punkte  und
und  identisch sein.
identisch sein.
Letzteres ist ein Widerspruch zur Wahl von  .
. ist nämlich der Mittelpunkt von
ist nämlich der Mittelpunkt von  .
.
Lösung 1
Ja, der Fall, dass 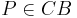 muss durchdacht werden, da die Lage des Punktes theoretisch überall im Schnittpunkt der Halbebenen ligen kann. Wenn man den zweiten Teil des Beweises (ohne Hilfskonstruktion) betrachtet, ist die (mögliche) Lage von
muss durchdacht werden, da die Lage des Punktes theoretisch überall im Schnittpunkt der Halbebenen ligen kann. Wenn man den zweiten Teil des Beweises (ohne Hilfskonstruktion) betrachtet, ist die (mögliche) Lage von  nicht sofort ersichtlich.
nicht sofort ersichtlich.
Allerdings kann man auch begründen: Nein, man muss den Fall nicht aufführen, da es trivial ist, die Lage von 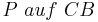 zu widerlegen. Man kann es sich bildlich so vorstellen, dass
zu widerlegen. Man kann es sich bildlich so vorstellen, dass  ja mithilfe des Mittelpunktes der Strecke
ja mithilfe des Mittelpunktes der Strecke  konstruiert wurde und deshalb - sollte
konstruiert wurde und deshalb - sollte 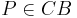 sein - die Strahlen
sein - die Strahlen 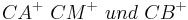 identisch seien.
--Heinzvaneugen 21:16, 11. Jul. 2010 (UTC)
identisch seien.
--Heinzvaneugen 21:16, 11. Jul. 2010 (UTC)
Lösung 2
Wenn wir mit einem indirekten Beweis zeigen dass P nicht in der Halbebene 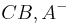
liegen kann (haben wir), so gilt das für die komplette GESCHLOSSENE Halbebene 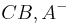
d.h. auch für die Trägergerade CB.
Wir wissen also schon dass P nicht auf CB liegen kann, dieser Teil ist also überflüssig...
--Principella 19:59, 19. Jul. 2010 (UTC)
Frage
Unabhängig von der Aufgabenstellung mal: Müsste ich falls ich das zeigen müsste nich auch genau so zeigen, dass P nicht auf der Geraden AB liegen kann? --TheGeosi 08:24, 21. Jul. 2010 (UTC)
In diesem Fall definitiv nicht, aber es kommt immer drauf an wie wir den Beweis geführt haben. Wenn es ein indirekter Beweis ist, nehmen wir genau das an, was wir nicht wollen und schließen beim Widerspruch alles "Angenommene" automatisch aus. 1) ist zwar ein direkter Beweis, aber es ist dasselbe Prinzip. Wir sagen dass P NICHT in ein und derselben (geschlossenen) Halbebene mit C liegen kann (Begründung = Konstruktion von P), also bleibt nur noch eine Möglichkeit = P liegt in der OFFENEN Halbebene AB,C- (d.h. ohne AB) --Principella 11:28, 21. Jul. 2010 (UTC)
Ich denke auch, dass wir das nicht beweisen müssen, da wir nach Konstruktion P und C in verschiedene Halbebenen bezüglich AB gesteckt haben. Die Frage, ob P auf CB liegt geht ja ein wenig in die selbe Richtung, kann also von der Konstruktion abgeleitet werden. In dem Fall (Frage, ob P auf AB liegen kann) ist es jedoch sofort einsichtig! --Heinzvaneugen 12:36, 21. Jul. 2010 (UTC)

