Lösung von Aufgabe 5.5 P (SoSe 20): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Untersuchen Sie folgende Relation ''S'' auf ihre Eigenschaften:<br /> <math>\ g S h \Leftrightarrow \ g \cap h \neq \lbrace \rbrace </math><br /> Kategor…“) |
|||
| Zeile 3: | Zeile 3: | ||
| + | g geschnitten g gleich g (ungleich leere Menge) => reflexiv --[[Benutzer:Kohlhoffj|tgksope]] ([[Benutzer Diskussion:Kohlhoffj|Diskussion]]) | ||
| + | wenn g geschnitten h ungleich leere Menge ist, ist auch h geschnitten g ungleich leere Menge => symmetrisch --[[Benutzer:Kohlhoffj|tgksope]] ([[Benutzer Diskussion:Kohlhoffj|Diskussion]]) | ||
| + | |||
| + | es sei: g={2} und h={2,4} und d={4} => g geschnitten h = {2}; h geschnitten d = {4} und g geschnitten d = {} => nicht transitiv --[[Benutzer:Kohlhoffj|tgksope]] ([[Benutzer Diskussion:Kohlhoffj|Diskussion]]) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Aktuelle Version vom 21. Mai 2020, 13:07 Uhr
Untersuchen Sie folgende Relation S auf ihre Eigenschaften:
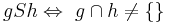
g geschnitten g gleich g (ungleich leere Menge) => reflexiv --tgksope (Diskussion)
wenn g geschnitten h ungleich leere Menge ist, ist auch h geschnitten g ungleich leere Menge => symmetrisch --tgksope (Diskussion)
es sei: g={2} und h={2,4} und d={4} => g geschnitten h = {2}; h geschnitten d = {4} und g geschnitten d = {} => nicht transitiv --tgksope (Diskussion)

