Lösung von Aufg. 6.3P (SoSe 20): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex. Kategorie:Geo_P“) |
|||
| Zeile 2: | Zeile 2: | ||
| + | Voraussetzung: zwei konvexe Punktmengen | ||
| + | Behauptung: Durchschnitt dieser Mengen ist konvex | ||
| + | |||
| + | Zusatz: Es seien die Punkte A und B, mit <math>(A \epsilon M,N) \wedge (B \epsilon M,N)</math>. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! || Beweisschritt !! Begründung | ||
| + | |- | ||
| + | | 1) || <math>(A,B \epsilon M,N)</math> || Zusatz | ||
| + | |- | ||
| + | | 2) || <math>(A,B \epsilon M)</math> || 1) | ||
| + | |- | ||
| + | | 3) || <math>(Strecke AB \epsilon M)</math> || 2), Voraussetzung | ||
| + | |- | ||
| + | | 4) || <math>(A,B \epsilon N)</math> || 1) | ||
| + | |- | ||
| + | | 5) || <math>(Strecke AB \epsilon N)</math> || 4), Voraussetzung | ||
| + | |- | ||
| + | | 6) || <math>(Strecke AB \epsilon (N \cap M))</math> || 3), 5) | ||
| + | |- | ||
| + | | 7) || <math>(A,B \epsilon (N \cap M)\Rightarrow (Strecke AB \epsilon (N \cap M)))</math> || 1)-6) (Zusammenfassung der Folgerungen) | ||
| + | |- | ||
| + | | 8) || <math>(N \cap M)</math> ist konvex || 7), Definition konvex | ||
| + | |} | ||
| + | --[[Benutzer:Kohlhoffj|tgksope]] ([[Benutzer Diskussion:Kohlhoffj|Diskussion]]) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Version vom 28. Mai 2020, 18:43 Uhr
Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex.
Voraussetzung: zwei konvexe Punktmengen
Behauptung: Durchschnitt dieser Mengen ist konvex
Zusatz: Es seien die Punkte A und B, mit 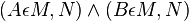 .
.
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | 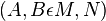 |
Zusatz |
| 2) | 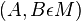 |
1) |
| 3) | 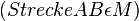 |
2), Voraussetzung |
| 4) | 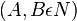 |
1) |
| 5) | 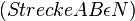 |
4), Voraussetzung |
| 6) | 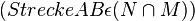 |
3), 5) |
| 7) | 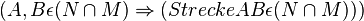 |
1)-6) (Zusammenfassung der Folgerungen) |
| 8) | 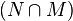 ist konvex ist konvex |
7), Definition konvex |
--tgksope (Diskussion)

