Lösung von Aufg. 7.3P (SoSe 20): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Gegeben seien drei paarweise verschiedene und '''kollineare''' Punkte ''A'', ''B'' und ''C'' in einer Ebene ''E''. Ferner sei eine Gerade ''g'' Teilmenge der E…“)
 
Zeile 4: Zeile 4:
  
  
 +
Voraussetzung: <math>(\overline {AB} \cap g = \emptyset )\wedge (\overline {BC} \cap g = \emptyset )</math>
  
 +
Behauptung: <math>\overline {AC} \cap g = \emptyset </math>
  
 +
Annahme: <math>\overline {AC} \cap g \neq \emptyset </math>
 +
 +
{| class="wikitable"
 +
|-
 +
!  || Beweisschritt !! Begründung
 +
|-
 +
| 1) || <math>A \epsilon gA+ \wedge C\epsilon gA-</math> || Annahme, Satz von Pasch
 +
|-
 +
| 2) || <math>A \epsilon gA-</math> || 1), Voraussetzung, Satz von Pasch
 +
|-
 +
| 3) || <math>(\overline {AB} \cap g \neq \emptyset)</math> || 1), 2), Satz von Pasch
 +
|-
 +
| 4) || Widerspruch zur Voraussetzung || 3), Voraussetzung
 +
|}
 +
--[[Benutzer:Kohlhoffj|tgksope]] ([[Benutzer Diskussion:Kohlhoffj|Diskussion]])
 +
 +
Frage: Wie kann ich + und - "hochstellen"? --[[Benutzer:Kohlhoffj|tgksope]] ([[Benutzer Diskussion:Kohlhoffj|Diskussion]])
  
  
 
[[Kategorie:Geo_P]]
 
[[Kategorie:Geo_P]]

Version vom 8. Juni 2020, 16:58 Uhr

Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:

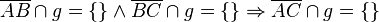
\overline{AB}\cap g=\lbrace \rbrace \wedge \overline{BC}\cap g=\lbrace \rbrace\Rightarrow \overline{AC}\cap g=\lbrace \rbrace

(Hinweis: Nehmen Sie einen weiteren Punkt D an, mit 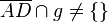\overline{AD}\cap g\not=\lbrace \rbrace und nutzen Sie den Satz von Pasch)


Voraussetzung: 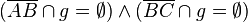(\overline {AB} \cap g = \emptyset )\wedge (\overline {BC} \cap g = \emptyset )

Behauptung: 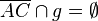\overline {AC} \cap g = \emptyset

Annahme: 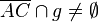\overline {AC} \cap g \neq \emptyset

Beweisschritt Begründung
1) 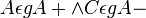A \epsilon gA+ \wedge C\epsilon gA- Annahme, Satz von Pasch
2) 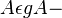A \epsilon gA- 1), Voraussetzung, Satz von Pasch
3) 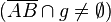(\overline {AB} \cap g \neq \emptyset) 1), 2), Satz von Pasch
4) Widerspruch zur Voraussetzung 3), Voraussetzung

--tgksope (Diskussion)

Frage: Wie kann ich + und - "hochstellen"? --tgksope (Diskussion)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._7.3P_(SoSe_20)&oldid=35515“