Lösung von Aufgabe 11.1P (SoSe 20): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie Satz IX.4: Bei einer Punktspiegelung werden Geraden stets auf parallele Bildgeraden abgebildet.<br /> Kategorie:Geo_P“) |
|||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
Bei einer Punktspiegelung werden Geraden stets auf parallele Bildgeraden abgebildet.<br /> | Bei einer Punktspiegelung werden Geraden stets auf parallele Bildgeraden abgebildet.<br /> | ||
| + | Voraussetzung: Punktspiegelung einer Geraden g | ||
| + | Behauptung: g parallel zu g'' | ||
| + | Zusatz: a und b sind die Spiegelgeraden der Punktspiegelung mit: <math>a \cap b = S</math> und <math>a \cap g = P</math> und <math>b \cap g = E</math> | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! !! Beweisschritt!! Begründung | ||
| + | |- | ||
| + | | 1)|| <math>S_a\circ S_b(g)=g'' </math>|| Geradentreue der Geradenspiegelung, Def. Punktspiegelung | ||
| + | |- | ||
| + | | 2)|| <math>S_a\circ S_b(P)=P'' \wedge S_a\circ S_b(E)=E''</math> || Def. Punktspiegelung, S ist Fixpunkt | ||
| + | |- | ||
| + | | 3)|| <math> |< PSE| = |< P''SE''|=|< ab|</math>|| Winkelmaßerhaltung der Geradenspiegelung, 2), Zusatz | ||
| + | |- | ||
| + | | 4)|| <math> | PS | = | P''S | \wedge | ES | = | E''S |</math>|| Eigenschaft Punktspiegelung, 2) | ||
| + | |- | ||
| + | | 5)|| <math>g'' \cap a=P'' \wedge g'' \cap b=E''</math>|| 1), 2), 3), Eigenschaft Geradenspiegelung, Zusatz | ||
| + | |- | ||
| + | | 6)|| <math>g|| g''</math> || 3), 4), 5) | ||
| + | |} | ||
| + | --[[Benutzer:Kohlhoffj|tgksope]] ([[Benutzer Diskussion:Kohlhoffj|Diskussion]]) 10:58, 25. Jul. 2020 (CEST) | ||
| + | |||
| + | Der Beweis geht kürzer: | ||
| + | |||
| + | Voraussetzung: Punktspiegelung <math>S_a\circ S_b</math> mit <math> a \cap b = \lbrace S \rbrace</math> und a <math>\perp b </math> | ||
| + | Behauptung: g || g'' | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! !! Beweisschritt!! Begründung | ||
| + | |- | ||
| + | | 1)|| Drehen a und b mit festen S und festen Drehwinkel so, dass a II b || Punktspiegelung | ||
| + | |- | ||
| + | | 2)|| <math>S_a(g)=g' </math><math>, g' || g</math> || Parallelentreue, 1), Vor., Def. Geradenspiegelung | ||
| + | |- | ||
| + | | 3)|| <math> S_b(g')=g'' = g' </math>|| Def. Fixgerade, Vor. | ||
| + | |- | ||
| + | | 4)|| <math>g || g''</math> || 2), 3), Transitivität der Parallelenrelation | ||
| + | |- | ||
| + | |} | ||
| + | --[[Benutzer:Tutorin Laura|Tutorin Laura]] ([[Benutzer Diskussion:Tutorin Laura|Diskussion]]) 11:06, 27. Jul. 2020 (CEST) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Aktuelle Version vom 27. Juli 2020, 11:06 Uhr
Beweisen Sie Satz IX.4:
Bei einer Punktspiegelung werden Geraden stets auf parallele Bildgeraden abgebildet.
Voraussetzung: Punktspiegelung einer Geraden g
Behauptung: g parallel zu g
Zusatz: a und b sind die Spiegelgeraden der Punktspiegelung mit: 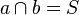 und
und 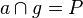 und
und 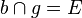
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | 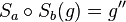 |
Geradentreue der Geradenspiegelung, Def. Punktspiegelung |
| 2) | 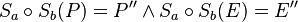 |
Def. Punktspiegelung, S ist Fixpunkt |
| 3) | 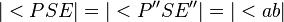 |
Winkelmaßerhaltung der Geradenspiegelung, 2), Zusatz |
| 4) | 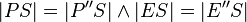 |
Eigenschaft Punktspiegelung, 2) |
| 5) | 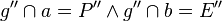 |
1), 2), 3), Eigenschaft Geradenspiegelung, Zusatz |
| 6) | 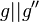 |
3), 4), 5) |
--tgksope (Diskussion) 10:58, 25. Jul. 2020 (CEST)
Der Beweis geht kürzer:
Voraussetzung: Punktspiegelungmit
und a
Behauptung: g || g
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | Drehen a und b mit festen S und festen Drehwinkel so, dass a II b | Punktspiegelung |
| 2) | 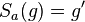 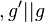 |
Parallelentreue, 1), Vor., Def. Geradenspiegelung |
| 3) | 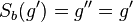 |
Def. Fixgerade, Vor. |
| 4) | 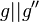 |
2), 3), Transitivität der Parallelenrelation |
--Tutorin Laura (Diskussion) 11:06, 27. Jul. 2020 (CEST)

