Lösungen Serie 1 WS 20/21: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 1: | Zeile 1: | ||
| − | |||
| − | |||
=Aufgabe 1.1 = | =Aufgabe 1.1 = | ||
| Zeile 72: | Zeile 70: | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
| + | ===Lösungsvorschlag=== http://geometrie.zum.de/wiki/Datei:Serie1.1.jpg http://geometrie.zum.de/wiki/Datei:Serie1.2.jpg | ||
Version vom 9. November 2020, 14:08 Uhr
Inhaltsverzeichnis |
Aufgabe 1.1
Definieren Sie die folgenden Begriffe aus der Mengenlehre:
| a) | Schnittmenge, |
| b) | Vereinigungsmenge, |
| c) | Teilmenge, |
| d) | Potenzmenge. |
Lösungen
Lösung 1
Lösung 2
Lösung 3
Aufgabe 1.2
| a) | Es sei  ein Kreis in Mittelpunktslage bezüglich eines kartesischen Koordinatensystems. Für den Radius ein Kreis in Mittelpunktslage bezüglich eines kartesischen Koordinatensystems. Für den Radius  von von  gelte gelte 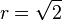 . .  sei die Menge aller Koordinatenpaare sei die Menge aller Koordinatenpaare 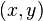 die Punkte von die Punkte von  beschreiben mit beschreiben mit 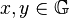 . Geben Sie . Geben Sie  in aufzählender Weise an. in aufzählender Weise an.
|
| b) | 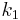 sei in Kreis mit dem Mittelpunkt sei in Kreis mit dem Mittelpunkt 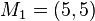 und dem Radius und dem Radius 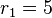 . . 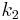 sei ein Kreis mit dem Mittelpunkt sei ein Kreis mit dem Mittelpunkt 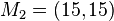 und dem Radius und dem Radius 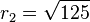 . Geben Sie die Menge . Geben Sie die Menge 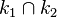 an. an.
|
Lösungen
Lösung 1
Lösung 2
Lösung 3
Aufgabe 1.3
Es sei 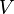 die Menge aller (konvexen) Vierecke.
die Menge aller (konvexen) Vierecke.
Ferner seien:
-
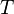 , die Menge aller Trapeze,
, die Menge aller Trapeze,
-
 , die Menge aller Parallelogramme,
, die Menge aller Parallelogramme,
-
 , die Menge aller symmetrischen Trapeze,
, die Menge aller symmetrischen Trapeze,
-
 , die Menge aller Rechtecke,
, die Menge aller Rechtecke,
-
 , die Menge aller Quadrate,
, die Menge aller Quadrate,
-
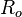 , die Menge aller Rauten und
, die Menge aller Rauten und
-
 , die Menge aller Drachen.
, die Menge aller Drachen.
| a) | Geben Sie zwei Vierecksmengen  und und  an, für die an, für die 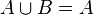 gilt. gilt.
|
| b) | Bestimmen Sie 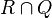 . .
|
| c) | Klaus behauptet: 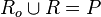 . Stimmt das? . Stimmt das?
|
| d) | Definieren Sie, was man unter einem Element von  versteht. versteht.
|
| e) | Bestimmen Sie 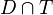 . .
|
Lösungen
Lösung 1
Lösung 2
Lösung 3
===Lösungsvorschlag=== http://geometrie.zum.de/wiki/Datei:Serie1.1.jpg http://geometrie.zum.de/wiki/Datei:Serie1.2.jpg

