Lösung von Aufgabe 1.2 (WS 20 21): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Geben Sie eine andere Schreibweise der folgenden Mengen an und prüfen Sie, welche Mengen identisch sind.<br /><br /> <math>M_1 = \{x\vert x\in \mathbb{N}\wedg…“)
 
 
(8 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt)
Zeile 7: Zeile 7:
 
<math>M_6 = \{x\vert x\in \mathbb{R}\wedge (x+2)^{2} = 0\}</math><br /><br />
 
<math>M_6 = \{x\vert x\in \mathbb{R}\wedge (x+2)^{2} = 0\}</math><br /><br />
  
 +
M1, M2, M4 und M6 sind leere Mengen, M3={-2}, M5={Wurzel 2; - Wurzel 2}
  
 +
M6 ist nicht gleich die leere Menge.
 +
Es wäre super, wenn du hinter deine Lösung deine Signatur angeben würdest.
 +
Gehe dafür in der Menüleiste auf erweitert und dann das vorletzte Symbol (der Stift) drücken. Danke! --[[Benutzer:Tutorin Laura|Tutorin Laura]] ([[Benutzer Diskussion:Tutorin Laura|Diskussion]]) 20:30, 9. Nov. 2020 (CET)
  
 +
 +
M1=M2=M4=∅
 +
<br />
 +
M3=M6={-2}
 +
<br />
 +
M5={<math>\sqrt 2</math>}    ''(bearbeitet)''
 +
<br />
 +
--[[Benutzer:Dwight Kurt Schrute|Dwight Kurt Schrute]] ([[Benutzer Diskussion:Dwight Kurt Schrute|Diskussion]]) 17:14, 3. Nov. 2020 (CET)
 +
 +
Hat M5 nur eine Lösung?--[[Benutzer:Tutorin Laura|Tutorin Laura]] ([[Benutzer Diskussion:Tutorin Laura|Diskussion]]) 09:06, 5. Nov. 2020 (CET)
 
[[Kategorie:Geo_P]]
 
[[Kategorie:Geo_P]]
 +
 +
M5={<math>\sqrt 2</math>, -  <math>\sqrt 2</math>}  --[[Benutzer:Hippoo|Hippoo]] ([[Benutzer Diskussion:Hippoo|Diskussion]]) 21:42, 5. Nov. 2020 (CET)
 +
Ja genau Hippoo. --[[Benutzer:Tutorin Laura|Tutorin Laura]] ([[Benutzer Diskussion:Tutorin Laura|Diskussion]]) 22:24, 6. Nov. 2020 (CET)

Aktuelle Version vom 9. November 2020, 20:30 Uhr

Geben Sie eine andere Schreibweise der folgenden Mengen an und prüfen Sie, welche Mengen identisch sind.

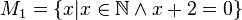
M_1 = \{x\vert x\in \mathbb{N}\wedge x+2 = 0\}

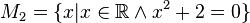
M_2 = \{x\vert x\in \mathbb{R}\wedge x^{2}+2 = 0\}

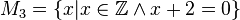
M_3 = \{x\vert x\in \mathbb{Z}\wedge x+2 = 0\}

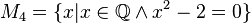
M_4 = \{x\vert x\in \mathbb{Q}\wedge x^{2}-2 = 0\}

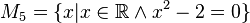
M_5 = \{x\vert x\in \mathbb{R}\wedge x^{2}-2 = 0\}

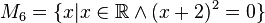
M_6 = \{x\vert x\in \mathbb{R}\wedge (x+2)^{2} = 0\}

M1, M2, M4 und M6 sind leere Mengen, M3={-2}, M5={Wurzel 2; - Wurzel 2} 

M6 ist nicht gleich die leere Menge. 
Es wäre super, wenn du hinter deine Lösung deine Signatur angeben würdest.
Gehe dafür in der Menüleiste auf erweitert und dann das vorletzte Symbol (der Stift) drücken. Danke! --Tutorin Laura (Diskussion) 20:30, 9. Nov. 2020 (CET)


M1=M2=M4=∅
M3=M6={-2}
M5={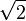\sqrt 2} (bearbeitet)
--Dwight Kurt Schrute (Diskussion) 17:14, 3. Nov. 2020 (CET) 

Hat M5 nur eine Lösung?--Tutorin Laura (Diskussion) 09:06, 5. Nov. 2020 (CET)

M5={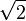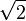\sqrt 2, - \sqrt 2} --Hippoo (Diskussion) 21:42, 5. Nov. 2020 (CET) 

Ja genau Hippoo. --Tutorin Laura (Diskussion) 22:24, 6. Nov. 2020 (CET)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_1.2_(WS_20_21)&oldid=36484“