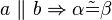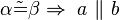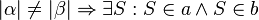Lösung von Aufgabe 4.3 (SoSe 22): Unterschied zwischen den Versionen

Aktuelle Version vom 15. Mai 2022, 19:40 Uhr

a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel und . Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äquivalente Aussage (Begründen Sie jeweils)?

a) der Stufenwinkelsatz lautet: wenn zwei parallele Geraden a und b von einer dritten Geraden c geschnitten werden, so sind die auftretenden Stufenwinkel gleich groß--Kwd077 (Diskussion) 16:12, 10. Mai 2022 (CEST) b) 1. Stufenwinkelsatz, wenn zwei parallele Geraden a und b geschnitten werden von einer Geraden c, dann sind die auftretenden Stufenwinkel gleich

     groß
  2. Umkehrung des Stufenwinkelsatzes, wenn beim Schneiden zweier Geraden a und b mit einer Geraden c die auftretenden Stufenwinkel gleich groß sind, 
     dann sind die Geraden a und b parallel zueinander
  3. Kontraposition des Stufenwinkelsatzes, wenn die Stufenwinkel alpha und beta nicht kongruent, dann existiert ein  Schnittpunkt S, wobei S 
     Element ais a als auch Element aus b ist.
  4. Äquivalenzaussage, genau dann wenn die beiden parallelen Geraden a und b von einer Geraden c geschnitten werden, sind die Stufenwinkel alpha und 
     beta kongruent zueinander--Kwd077 (Diskussion) 16:12, 10. Mai 2022 (CEST)

Du hast alle Aussagen richtig benannt. Du kannst dir noch überlegen, ob Umkehrung, Kontraposition und Äquivalenzaussage generell äquivalent zu jedmöglicher ursprünglichen Aussage sind. --Matze2000 (Diskussion) 20:40, 15. Mai 2022 (CEST)