Übung Aufgaben 6 (SoSe 23): Unterschied zwischen den Versionen
(→Aufgabe 6.2) |
|||
| Zeile 1: | Zeile 1: | ||
| − | ==Aufgabe 6.1== | + | == Aufgabe 6.1 == |
| − | + | a) Formulieren Sie die Kontraposition der Umkehrung des Stufenwinkelsatzes<br /> | |
| − | + | b) Formulieren sie die Umkehrung der Kontraposition des Stufenwinkelsatzes<br /> | |
[[Lösung von Aufg. 6.1P (SoSe_23)]] | [[Lösung von Aufg. 6.1P (SoSe_23)]] | ||
| + | |||
==Aufgabe 6.2== | ==Aufgabe 6.2== | ||
| − | + | Geben Sie eine formal korrekte Definition für die Halbgerade <math>\ AB^-</math> an, ohne die Zwischenrelation zu verwenden. | |
| − | + | ||
| − | + | ||
[[Lösung von Aufg. 6.2P (SoSe_23)]] | [[Lösung von Aufg. 6.2P (SoSe_23)]] | ||
== Aufgabe 6.3 == | == Aufgabe 6.3 == | ||
| − | + | Das Parallelenaxiom lautet wie folgt:<br /> | |
| + | Zu jeder Geraden ''g'' und zu jedem nicht auf ''g'' liegenden Punkt ''A'' gibt es höchstens eine Gerade, die durch ''A'' verläuft und zu ''g'' parallel ist.<br /> | ||
| + | Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:<br /> | ||
| + | Es seien ''a'', ''b'' und ''c'' drei paarweise verschiedene Geraden in ein und derselben Ebene.<br /> | ||
| − | + | a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: <math>\ a \| b \wedge b \| c \Rightarrow \ a \| c</math> . <br /> | |
| − | + | b) Welche Eigenschaft der Relation <math>\| </math> auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?<br /> | |
| − | + | [[Lösung von Aufg. 6.3_P (SoSe_23)]] | |
| − | + | ||
| + | ==Aufgabe 6.4 == | ||
| + | Definieren Sie den Begriff: "konvexe Punktmenge" indem Sie die verbal formulierte Definition (siehe [[Halbebenen_und_der_Satz_von_Pasch_SoSe_23#Konvexe_Punktmengen|Wiki-Skript)]] in eine geeignete "Mengenschreibweise" übersetzen.<br /> | ||
| + | '''''M'' ist konvex, wenn gilt: ...''' | ||
[[Lösung von Aufg. 6.4P (SoSe_23)]] | [[Lösung von Aufg. 6.4P (SoSe_23)]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Version vom 22. Mai 2023, 11:06 Uhr
Inhaltsverzeichnis |
Aufgabe 6.1
a) Formulieren Sie die Kontraposition der Umkehrung des Stufenwinkelsatzes
b) Formulieren sie die Umkehrung der Kontraposition des Stufenwinkelsatzes
Lösung von Aufg. 6.1P (SoSe_23)
Aufgabe 6.2
Geben Sie eine formal korrekte Definition für die Halbgerade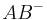 
an, ohne die Zwischenrelation zu verwenden.
Lösung von Aufg. 6.2P (SoSe_23)
Aufgabe 6.3
Das Parallelenaxiom lautet wie folgt:
Zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt A gibt es höchstens eine Gerade, die durch A verläuft und zu g parallel ist.
Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:
Es seien a, b und c drei paarweise verschiedene Geraden in ein und derselben Ebene.
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: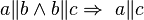 
.
b) Welche Eigenschaft der Relation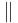 
auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
Lösung von Aufg. 6.3_P (SoSe_23)
Aufgabe 6.4
Definieren Sie den Begriff: "konvexe Punktmenge" indem Sie die verbal formulierte Definition (siehe Wiki-Skript) in eine geeignete "Mengenschreibweise" übersetzen.
M ist konvex, wenn gilt: ...
Lösung von Aufg. 6.4P (SoSe_23)
