Die Arbeitsblätter: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Arbeitsblatt 1: Freier Fall) |
*m.g.* (Diskussion | Beiträge) (→Koordinaten bei der Kreisbewegung) |
||
| (18 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | =Arbeitsblatthilfe: Raster= | ||
| + | [[Datei:QrRaster.pdf|Rastercode]]<br /> | ||
| + | |||
| + | [[Datei:Raster.pdf|Raster]] | ||
| + | |||
=Arbeitsblatt 1: Freier Fall= | =Arbeitsblatt 1: Freier Fall= | ||
[[Datei:ArbeitsblattFreierFall.pdf|Mit Parabel fitten]] | [[Datei:ArbeitsblattFreierFall.pdf|Mit Parabel fitten]] | ||
| Zeile 5: | Zeile 10: | ||
https://www.geogebra.org/m/z5e3t2qd | https://www.geogebra.org/m/z5e3t2qd | ||
[[Kategorie: PhysikGieding]] | [[Kategorie: PhysikGieding]] | ||
| + | |||
| + | =Arbeitsblatt 2: Der Zusammenhang zwischen Geschwindigkeit und Zeit beim freien Fall= | ||
| + | ==Die Geogebra Experimentierumgebung== | ||
| + | <ggb_applet id="cdst3jhc" width="1400" height="1000" /><br /> | ||
| + | Der direkte Link zu dieser APP in der Geogebra Cloud:<br /> | ||
| + | https://www.geogebra.org/m/cdst3jhc | ||
| + | ==Die Aufgaben== | ||
| + | Durch Messungen hatten wir festgestellt, dass das Weg-Zeit-Gesetz des freien Falls sich durch die folgende Gleichung beschreiben lässt: <math>s=\frac{g}{2}t^2</math><br /> | ||
| + | Die entsprechende Kurve (Parabel) wurde mittels Geogebra in der obigen App gezeichnet. Gewisse Überlegungen ließen uns zu dem Schluss kommen, dass die Geschwindigkeit zu einem Zeitpunkt t wohl der Anstieg der Tangente zu diesem Zeitpunkt an die Parabel ist. Euer Auftrag besteht jetzt darin, mittels des Schiebereglers für die Zeit die Zeitpunkte 0s;0,1s;0,2s;0,3s;0,4s;0,5s;0,6s einzustellen und den zugehörigen Anstieg der Tangente abzulesen. Tragt die zusammengehörigen Werte für Zeit und Anstieg in eine Wertetabelle ein und lasst das Geschwindigkeit-Zeit-Diagramm für diese Wertetabelle zeichnen. Welchen Zusammenhang zwischen Geschwindigkeit und Zeit vermutest Du? | ||
| + | ==Das Arbeitsblatt zum Ausdrucken bzw. Herunterladen== | ||
| + | [[Datei:Arbeitsblatt v t freier Fall.pdf|Geschwindigkeit-Zeit-Gesetz freier Fall]] | ||
| + | =Arbeitsblatt 3= | ||
| + | ==Beschleunigung== | ||
| + | [[Datei:QR 27 11 23.pdf|qrCode]]<br /> | ||
| + | |||
| + | [[Datei:AB 03.pdf|Beschleunigung]] | ||
| + | =Arbeitsblatt 5= | ||
| + | ==Schiefe Ebene== | ||
| + | Adresse: http://geometrie.zum.de/wiki/Die_Arbeitsbl%C3%A4tter#Schiefe_Ebene<br /> | ||
| + | |||
| + | [[Datei:QR AB05.pdf|QR Code AB 05]]<br /> | ||
| + | |||
| + | [[Datei:AB 05.pdf|schiefe Ebene]] | ||
| + | =Arbeitsblatt 6= | ||
| + | ==Fallzeit und Winkelfunktionen== | ||
| + | [[Datei:QR AB06.pdf|QR Code AB 06]]<br /> | ||
| + | |||
| + | [[Datei:AB 06.pdf|AB 6 Sinus und Kosinus]] | ||
| + | =Arbeitsblatt 7= | ||
| + | ==Kreisbewegung== | ||
| + | [[Datei:QrCode 07.png|thumb|qrCode]]<br /> | ||
| + | |||
| + | [[Datei:Kreisbewegung.pdf|Kreisbewegung]] | ||
| + | =Arbeitsblatt 9= | ||
| + | ==Kreisbewegung== | ||
| + | [[Datei:qr_03.png|QR-Code]] | ||
| + | [[Datei:Kreisbewegung 3.pdf|Kreisbewegung]] | ||
| + | =Arbeitsblatt 10= | ||
| + | ==Koordinaten bei der Kreisbewegung== | ||
| + | [[Datei:Qr code Koordinaten.png|qr code koordinaten]]<br /> | ||
| + | |||
| + | [[Datei:Kreisbewegung Koordinaten.pdf|Koordinaten bei der Kreisbewegung]] | ||
Aktuelle Version vom 23. Juni 2024, 21:02 Uhr
Inhaltsverzeichnis |
Arbeitsblatthilfe: Raster
Arbeitsblatt 1: Freier Fall
Geogebra Experimentierumgebung
https://www.geogebra.org/m/g2cq8eey
https://www.geogebra.org/m/z5e3t2qd
Arbeitsblatt 2: Der Zusammenhang zwischen Geschwindigkeit und Zeit beim freien Fall
Die Geogebra Experimentierumgebung
Der direkte Link zu dieser APP in der Geogebra Cloud:
https://www.geogebra.org/m/cdst3jhc
Die Aufgaben
Durch Messungen hatten wir festgestellt, dass das Weg-Zeit-Gesetz des freien Falls sich durch die folgende Gleichung beschreiben lässt: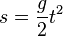 
Die entsprechende Kurve (Parabel) wurde mittels Geogebra in der obigen App gezeichnet. Gewisse Überlegungen ließen uns zu dem Schluss kommen, dass die Geschwindigkeit zu einem Zeitpunkt t wohl der Anstieg der Tangente zu diesem Zeitpunkt an die Parabel ist. Euer Auftrag besteht jetzt darin, mittels des Schiebereglers für die Zeit die Zeitpunkte 0s;0,1s;0,2s;0,3s;0,4s;0,5s;0,6s einzustellen und den zugehörigen Anstieg der Tangente abzulesen. Tragt die zusammengehörigen Werte für Zeit und Anstieg in eine Wertetabelle ein und lasst das Geschwindigkeit-Zeit-Diagramm für diese Wertetabelle zeichnen. Welchen Zusammenhang zwischen Geschwindigkeit und Zeit vermutest Du?
Das Arbeitsblatt zum Ausdrucken bzw. Herunterladen
Arbeitsblatt 3
Beschleunigung
Arbeitsblatt 5
Schiefe Ebene
Adresse: http://geometrie.zum.de/wiki/Die_Arbeitsbl%C3%A4tter#Schiefe_Ebene
Arbeitsblatt 6
Fallzeit und Winkelfunktionen
Arbeitsblatt 7
Kreisbewegung
Arbeitsblatt 9
Kreisbewegung
Arbeitsblatt 10
Koordinaten bei der Kreisbewegung
